45.З яких етапів складається перехід від одного опорного рішення до іншого.

Якщо одержаний варіант не оптимальний – будуємо наступну симплексну таблицю:

1) знаходимо ключовий елемент (стовбець з найменшою γ та рядок з найменшим співвідношенням b_i/a_ijk для всіх a_ijk > 0). Якщо елемента не існує – цільова функція має необмежене значення.

2) знаходимо елементи нової симплекс-таблиці методом Жордана-Гауса: елементи ключового рядка a_ij = a_ikj/a_ikjk, інші елементи a_ij = a_ij – (a_ikj*a_ijk)/a_ikjk.

3) складаємо нову сукупність базисних змінних: змінна ключового стовбця x_jk стає на місце базисної змінної x_ik.

46.Яким чином зберігається невід’ємність змінних нового базисного рішення.

Не понял вопроса, на консультации спрошу.

Применение М-задач

47.Що є критерієм оптимальності рішення ЗЛП в симплекс-методі.

Оптимальним вважається розвязок, якщо при F → min усі γ_j ≤ 0, або при F → max усі γ_j ≥ 0. Всі вільні змінні γ_j (останній рядок симплекс-таблиці) розраховуються за формулою .

48.Як визначається поточне значення цільової функції з таблиці?

Обчислимо значення цільової функції, відповідне до опорного плану, підставивши 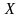у вираження (другий рядок таблиці). Одержимо .

49.Запишіть математичні моделі парі подвійних ЗЛП.

Початкова задача Zmin=CX; AX>=A0; X>=0 Двоїста задача: tmax=YA0; YA<=C; Y>=0

Початкова задача: Zmax=CX; AX<=A0; X>=0 Двоїста задача; tmin=YA0; YA>=C; Y>=0

50.Дайте економічну інтерпретацію парі подвійних завдань.

Економічна інтерперетація двоїстих задач. Нехай задана задача планування вир-ва(використання ресурсів). Модель№1.

Такій задачі відповідає двоїста задача:

Економічний зміст (3),(4). Уі-оцінка і-го ресурсу, при закупівлі усих ресурсів покупець намагається мінімізувати загальну ціну всих ресурсів. Обмеж.(4) означає, що ціна усих ресурсів, які ідуть на виготовлення одиниці продукції не менше ціни одиниці продукції. (1,2,3,4)-пари симетричних двоїстих задач.

51.Сформулюйте правила побудови подвійного завдання до початкової.

Розглянемо модель ЗЛП у загальній формі, у якій обмеження утворюють змішану систему, що полягає з нерівностей і рівностей, а змінні розділяються на вільні й невільні, тобто задачу:

при обмеженнях-нерівностях:

при обмеженнях-рівностях:

при ненегативних змінних:

при вільних змінних:

х_j 0 (j = t +1,…,n).

Двоїстої до даної прямої (вихідної) задачі називають задачу:

при ненегативних змінних:

при вільних змінних:

при обмеженнях-нерівностях:

при обмеженнях-рівностях:

т.е. задачу, одержувану з вихідної за наступними правилами:

1. Кількість змінних двоїстої задачі рівно m – числу обмежень вихідної задачі, а число обмежень двоїстої задачі рівно n – кількості змінних вихідної задачі.

2. Вільні члени 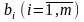вихідної задачі є коефіцієнтами цільової функції двоїстої задачі, а коефіцієнти цільової функції вихідної задачі стають правими частинами системи обмежень двоїстої задачі.

3. Матрицею коефіцієнтів системи обмежень двоїстої задачі служить матриця AT, одержувана транспонуванням матриці А коефіцієнтів системи обмежень вихідної задачі.

4. Кожному обмеженню-нерівності:

вихідної задачі відповідає ненегативна змінна:

двоїстої задачі, а кожному обмеженню-рівності:

відповідає вільна змінна:

yi 0

двоїстої задачі.

5. Кожної ненегативної змінної прямої задачі відповідає обмеження-нерівність:

двоїстої задачі з тим же знаком нерівності, а кожної вільної змінної х_j 0 відповідає обмеження-рівність:

двоїстої задачі.

6. Максимізація цільової функції вихідної задачі заміняється мінімізацією цільової функції двоїстої задачі.