30.Расстояние от точки до до прямой на плоскости и в пространстве.

В пространстве:

Теорема. Если задана точка М(х₀ , у₀ ), то расстояние до прямой Ах + Ву + С =0 определяется как

 

Доказательство. Пусть точка М ₁(х ₁, у ₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М₁ :

 

Координаты x₁ и у₁ могут быть найдены как решение системы уравнений:

(1)

Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М ₀ перпендикулярно заданной прямой.

Если преобразовать первое уравнение системы к виду:

A(x – x ₀ ) + B(y – y₀ ) + Ax₀ + By₀ + C = 0,

то, решая, получим:

Подставляя эти выражения в уравнение (1), находим:

На плоскости:

 Пусть прямая    на плоскости задана уравнением    и точка   имеет координаты    (рис. 25). Обозначим    – основание перпендикуляра, опущенного из точки    на прямую   ,  , _d – расстояние от точки    до прямой   . Тогда   , а    – нормальный вектор прямой. Рассмотрим скалярное произведение   . С одной стороны,   , так как   , следовательно, угол между ними   или   . С другой стороны,   , но точка  , поэтому ее координаты удовлетворяют уравнению   , откуда   , поэтому   . Приравнивая выражения, получим

 . Тогда    или

 .  (2.21)

 

Рис. 25

С помощью алгебраических уравнений в пространстве можно задавать не только поверхности, но и линии. Линию в пространстве естественно рассматривать как пересечение двух поверхностей, т.е. как геометрическое место точек, принадлежащих одновременно двум поверхностям.

31.Общее ур-ие плоскости и его исследование

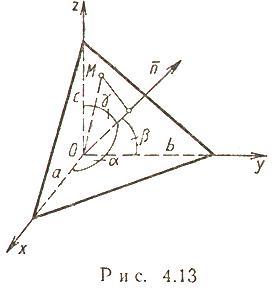
Общее уравнение плоскости (рис. 4.13) 

где   - нормальный вектор плоскости.

     В векторном виде  .

     Частные случаи общего уравнения плоскости:

     1) By + Cz + D = 0 - параллельна оси Ox;

     2) Ax + Cz + D = 0 - параллельна оси Oy;

     3) Ax + By + D = 0 - параллельна оси Oz;

     4) Cz + D = 0 - параллельна оси Oxy;

     5) By + D = 0 - параллельна оси Oxz;

     6) Ax + D = 0 - параллельна оси Oyz;

     7) Ax + By + Cz = 0 - проходит через начало координат;

     8) By + Cz = 0 - проходит через ось Ox;

     9) Ax + Cz = 0 - проходит через ось Oy;

     10) Ax + By = 0 - проходит через ось Oz;

     11) z = 0 - плоскость Oxy;

     12) y = 0 - плоскость Oxz;

     13) x = 0 - плоскость Oyz.

32.Взаимное расположение 2-х плоскостей

Возможны два случая взаимного расположения двух плоскостей в пространстве

1. Параллельны

2. Пересекаться

Опр. Две плоскости в пространстве называются параллельными, если они не пересекаются, в  противном случаи они пересекаются.

Теорема1: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Доказательство:

Пусть  и - данные плоскости, а1 и а2 - прямые в плоскости , пересекающиеся в точке А, в1 и в2 - соответственно параллельные им прямые в

плоскости . Допустим, что плоскости  и  не параллельны, т.е. пересекаются по некоторой прямой с. По теореме прямые а1 и а2, как параллельные прямым в1и в2, параллельны плоскости , и поэтому они не

пересекают лежащую в этой плоскости прямую с. Таким образом, в плоскости  через точку А проходят две прямые (а1 и а2) , параллельные прямой с. Но это невозможно по аксиоме параллельных. Мы пришли к противоречию ЧТД.

Перпендикулярные плоскости: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Теорема2: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Доказательство:

Пусть  - плоскость, в -перпендикулярная ей прямая,  - плоскость, проходящая через прямую в, с - прямая, по которой пересекаются плоскости  и . Докажем, что плоскости  и  перпендикулярны. Проведем в плоскости  через точку пересечения прямой в с плоскостью  прямую а,

перпендикулярную прямой с. Проведем через прямые а и в плоскость . Она перпендикулярна прямой с, т.к. прямая с перпендикулярна прямым а и в. Т. к. прямые а и в перпендикулярны, то плоскости  и  перпендикулярны. ч.т.д.