24.Уравнение спроса.Ур-е предложения.Точка равновес.Цены

25.Деление отрезка в заданном отношении.

Если точка М(x; y) лежит на прямой, проходящей через две данные точки  ( ,  ) и  ( ,  ), и дано отношение  , в котором точка М делит отрезок  , то координаты точки М определяются по формулам

,  .

Если точка М является серединой отрезка  , то ее координаты определяются по формулам

,  .

26.Вывод ур-ия окр-ти.

       Если точка С - центр окружности, R - ее радиус, а M - произвольная точка окружности, то из определения окружности следует, что  . Последнее равенство есть характеристическое уравнение окружности радиуса R с центром в точке C.

       Пусть на плоскости задана прямоугольная декартова система координат и точка C(a;b)- центр окружности радиуса R. Пусть М(х;у) - произвольная точка этой окружности. Как известно, расстояние  , поэтому уравнение можно записать так:

       или

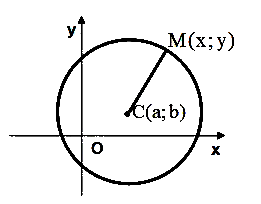
27.Вывод ур-ия эллипса

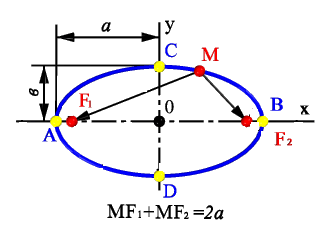
Эллипсом называется геометрическое место всех точек плоскости, сумма расстояний от которых до фокусов есть величина постоянная, большая, чем расстояние между фокусами.

Обозначим фокусы эллипса буквами   и  . Расстояние между ними - фокальное расстояние  ,   и  . Если М(х;у) - произвольная точка эллипса, то по определению эллипса   - характеристическое уравнение эллипса .

        Введем систему координат:  ,   и  . Тогда фокусами будут точки   и  .

        Пусть М(х;у) - любая точка эллипса, тогда

 

        Запишем характеристическое уравнение эллипса в координатной форме:

        Преобразуем равенство:

        Перенесем в левую часть равенства выражение, содержащее корень:

        Так как а>с, то  . Пусть  , то

 - каноническое уравнение эллипса .

28.Вывод ур-ия гиперболы

 Пусть расстояние между фокусами   и   гиперболы равно 2с , а абсолютная величина разности расстояний от точки гиперболы до фокусов равна   . Тогда гипербола в выбранной выше системе координат имеет уравнение

где

        Доказательство.     Пусть M(х;у)  -- текущая точка гиперболы (рис. 12.9).

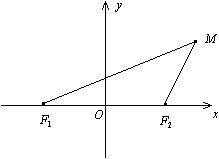
Так как разность двух сторон треугольника меньше третьей стороны, то   , то есть   ,   . В силу последнего неравенства вещественное число b , определяемое формулой  существует.

По условию, фокусы --   ,   . По формуле  для случая плоскости получаем

По определению гиперболы

Это уравнение запишем в виде

Обе части возведем в квадрат:

После приведения подобных членов и деления на 4, приходим к равенству

Опять обе части возведем в квадрат:

Раскрывая скобку и приводя подобные члены, получим

С учетом формулы  уравнение принимает вид

Разделим обе части уравнения на   и получим уравнение 

29.Вывод уравнения параболы

Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, н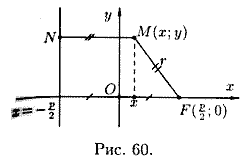 азываемой директрисой. Расстояние от фокуса F до директрисы называется параметром параболы и обозначается через p (p > 0).

Для вывода уравнения параболы выберем систему координат Оху так, чтобы ось Ох проходила через фокус F перпендикулярно директрисе в направлении от директрисы к F, а начало координат О расположим посередине между фокусом и директри­сой (см. рис. 60). В выбранной системе фокус F имеет координаты  , а уравнение директрисы имеет вид  х=-р/2.

Пусть М(х;у) — произвольная точка параболы. Соединим точку Μ с F. Проведем отрезок ΜΝ пер­пендикулярно директрисе. Согласно определению параболы MF = ΜΝ. По формуле расстояния между двумя точками на­ходим:

Следовательно,

Возведя обе части уравнения в квадрат, получим

т. е.

                                        

Уравнение называется каноническим уравнением параболы. Парабола есть линия второго порядка.