18. Полярная система координат.
Полярными координатами точки P называются радиус-вектор ρ - расстояние от точки P до заданной точки O (полюса) и полярный угол φ - угол между прямой OP и заданной прямой, проходящей через полюс (полярной осью). Полярный угол считается положительным при отсчете от полярной оси против часовой стрелки и отрицательным при отсчете в обратную сторону.
Координатные линии в полярных системах - окружности с центром в полюсе и лучи.
Формулы для перехода от полярных координат к декартовым
x=ρ*cos(φ), y=ρ*sin(φ)
и обратно:
ρ=√ (x2)+y2), φ=arctg(y/x)=arcsin(y/ρ)
Полярными
координатами произвольной точки P
(относительно заданной системы)
называются числа p=OP
и O=уголАОР
(см. рис.). Угол О при этом следует
понимать так, как принято в тригонометрии.
Число р называется первой координатой,
или полярным углом точки Р ( называются
также амплитудой).
Полярный
угол О имеет бесконечно много
возможных значений (отличающихся друг
от друга на величину вида 
,
где n - целое положительное число).
Значение полярного угла, удовлетворяющее
неравенствам 
,
называется главным.
19.Понятие вектора.Линейные операции над векторами.
Вектор - направленный отрезок.
Действия:
1)Суммой векторов a и b наз-ся вектор,кот.расположен от начала а в конец b.
Свойства сложения:
1. a + b = b + a.2. (a+b)+c=a+(b+c). 3 Для любого вектора a существует нулевой вектор О такой, что a+О=а. 4. Для каждого вектора a существует противоположный ему вектор a/ такой, что а+а/=О.
2) Разность a-b, это такой третий вектор a-b, который представляет сумму a и вектор противоположного b. (a+(-b))
3) Произведением вектора а на скаляр (число) λ называется вектор λ*а (или а*λ), который имеет длину |λ|*|а|, коллинеарен вектору а, имеет направление вектора а, если λ>0 и противоположное направление, если λ<0.
Свойства умножения вектора на число:
1. k(a + b) = ka + kb.
2. (k + m)a = ka + ma.
3. k(ma) = (km)a.
4.1*а=а
20.Скалярное произведение и его св-ва.
Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними:
ab = |a||b| cosφ .
Обозначения скалярного произведения: ab, (ab), a·b
Свойства:
ab =
0 
a 
b..
ab = ba .
(ka)b = k(ab).
(a + b)c = ac + bc .
a2 = aa = |a|2 , где а2 называется скалярным квадратом вектора а.
если ab>0=>угол остр.
если ab<0=>угол тупой
21.Векторное произведение и его св-ва
Векторным произведением векторов a и b на-ся вектор c, удовлетворяющий следующим условиям:
1)
,
где ϕ
- угол между векторами a
и b,
2) вектор c ортогонален векторам a и b
3) a, bи cобразуют правую тройку векторов.
Обозначается:
c=a*b
или
.
Свойства:
1)
;
2)
,
если a
пар-ен b
или a=
0 или b=
0;
3) (ma)*b= a*(mb) = m(a*b);
4) a*(b+ c) = a*b+ a* c;
5) Если заданы векторы a(xa, ya, za) и b(xb, yb, zb) в декартовой прямоугольной системе координат с единичными векторами I,j,k, то
*
=
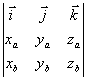
6) Геометрическим
смыслом векторного произведения
векторов является площадь параллелограмма,
построенного на векторах aи
b.
,
