1

.матрицы и их классификация.

Матрица-прямоуг.табл.чисел,имеющая m строк и n столбцов.эти числа наз-ся элементами матрицы.

Квадратная-матрица n-го порядка размера mна n

Диагональная-квадратная матрица, у которой все элементы вне главной диагонали равны нулю.

Единичной (обозначается Е иногда I) называется диагональная матрица с единицами на главной диагонали.

Нулевой называется матрица, все элементы которой равны нулю.

Скалярная-диагональная матрица,у кот.все элементы гл.диагонали равны нулю.

2.Действия с матрицами

Сложение матриц

Суммой двух матриц одного размера называется матрица того же размера, каждый элемент которой равен сумме соответствующих (т.е. стоящих на одинаковых местах) элементов данных матриц.

Можно складывать матрицы одинаковой размерности

Произведение

Произведением матрицы А на матрицу В наз-я матрица С,элемент которой равен скалярному произведению i-ой строки матрицыА на j-ый столбец матрицыВ.

Можно умножать только те, матрицы у которых число столбцов 1-ой равно числу строк 2-ой

Умножение на число

Произведением матрицы А на число Л называется матрица того же размера, каждый элемент которой равен произведению соответствующего элемента данной матрицы на это число.

Транспонирование

-операция, когда строки и столбцы меняются местами.

3.Обратная матрица

Матрица В наз-ся обратной,для матрицы А,если произведение этих матриц коммуникативно и равно един-ой матрице(АВ=ВА=Е).(понятие вводитс только для квадратных матриц)

Теорема. Для того чтобы квадратная матрица A имела обратную, необходимо и достаточно, чтобы её определитель был отличен от нуля.

Алгоритм нахождения:

1. . Убедиться, что определитель матрицыА не равен0.

2. Транспонировать матр А

3. Вычислить алг.допол.для новой матрицы

4. Сост-ть Аˉ¹ по формуле:

А₁₁А₁₂А₁₃

…………..

А₁ₓА₂ₓА₃ₓ

Фор-ой(4)можно пользоваться,если не делать(2),если делать п.2,то формула:

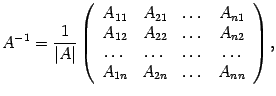
4.Определители2и 3 порядков

Определителем 2-го порядка называется число равное разности произведений элементов главной и второй диагонали:

Определителем третьего порядка наз-ся след-ее выражение:

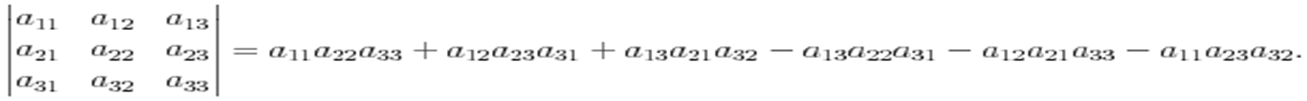
Правило «звезды»:

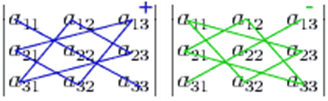
со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной в противоположного угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольников, построенных относительно этой диагонали. Следующая схема демонстрирует это правило, называемое правилом треугольников. В схеме синим (слева) отмечены элементы, чьи произведения идут со знаком плюс, а зеленым (справа) - со знаком минус.

5.Минор и алгебраическое дополнение.

Минором элемента матрицы n-го порядка называется определитель матрицы (n-1)-го порядка, полученный из матрицы А вычеркиванием i-й строки и j-го столбца.

Алгебраическим дополнением Аij элемента аij матрицы n-го порядка называется его минор, взятый со знаком, зависящий от номера строки и номера столбца:

то есть алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца – четное число, и отличается от минора знаком, когда сумма номеров строки и столба – нечетное число.

6.Свойства определителей.

1. Если какая-то строка (столбец) состоит из одних нулей, то определитель=0

2. Если какой-то ряд определ. Умножить на одно и тоже число, то и величина определителя умножится на это число.

3. А = АТ

Величина определителя при транспонировании не меняется.

4. Если в определителе есть 2 одинаковых ряда, то он = 0

5. Тоже св-во, если ряды пропорциональны

6. Величина определителя НЕ изменяется, если к элементам какой-то строки прибавится элементы др. строки, умноженные на одно и тоже число.

7. Если элементы какого-то ряда умножить на алгебраические дополнения элементов параллельного ряда, то определитель = 0