
- •1.Задачи статистики и ее организация в рф и за рубежом.
- •Основные итоги переписи 2010 в сравнении с 2002
- •Категории населения:
- •Балансовые уравнения численности населения:
- •По национальному составу и гражданству
- •Виды движения населения
- •Относительные показатели
- •Коэффициенты смертности
- •Коэффициент естественного прироста
- •Коэффициенты брачности /разводимости
- •Коэффициенты естественного движения населения
- •Коэффициенты смертности
- •Коэффициент естественного прироста
- •Коэффициенты брачности /разводимости Коэффициенты механического движения
- •Число прибывших
- •Число выбывших
- •Коэффициент прибытия: (‰)
- •Общее увеличение численности населения.
Билет №1
Предмет и метод статистики, связь с другими науками.
Статистикой называют различного рода числовые (цифровые) данные, характеризующие различные стороны жизни государства: политические отношения, культуру, производство и т.п.
Статистика – наука, рассматривающая совокупность методов, с помощью которых можно исследовать ту или иную конкретную совокупность социально-экономических явлений.
Статистика как наука имеет специфический предмет изучения. Предметом статистического изучения выступают совокупности – множества однокачественных варьирующих явлений. В это определение совокупности входят 3 основные категории:
Множество явлений;
Множество явлений, объединенных общим качеством, представляющих собой проявление одной и той же закономерности;
Множество варьирующих явлений, отличающихся по своим характеристикам.
Именно последнее свойство вызывает необходимость изучения всего множества явлений данного вида.
Статистикой разработаны и применяются специфические приемы, который в совокупности образуют ее методологию, например, метод массовых наблюдений, индексный метод и т.д.
Понятие «метод» статистики можно определить как совокупность приемов, применяемых ее для познания своего предмета. Он предполагает:
Разработку гипотезы;
Сбор данных (статистическое наблюдение);
Их обобщение (группировку и сводку);
Анализ результатов.
К основным методам относятся:
Диалектический метод (явления рассматриваются в развитии);
Метод статистических группировок (позволяет выделить в изучаемой совокупности соц-эк типы)
Метод массового статистического наблюдения (обеспечивает полноту инф)
Табличный и графический метод (наглядность)
Сама статистика выступает методом познания и для других наук.
Билет №2
1.Задачи статистики и ее организация в рф и за рубежом.
Общие принципы организации государственной статистики в РФ.
Преобразования в российской экономике, связанные с рыночными реформами, в значительной степени увеличивают потребности управляющих структур в современной и достоверной информации по различным аспектам жизнедеятельности общества.
В настоящее время роль государственной статистики трудно переоценить. Согласно статье 71 Конституции РФ официальный статистический учет находится в ведении Российской Федерации. Госкомстат России является официальным органом исполнительной власти, осуществляющим межотраслевую координацию и функциональное регулирование в сфере гос статистики. Госкомстат издает постановления, указы, распоряжения и иные нормативные акты, в том числе совместно с другими органами исполнительной власти. Госкомстат формирует официальную статистическую информацию на основе данных, получемых как от хозяйствующих субъектов и граждан, так и от федеральных и территориальных органов гос власти и местного самоуправления. Он ежегодно разрабатывает и вносит в Правительство РФ программу статистических работ.
Задачи органов государственной статистики.
Основные задачи Госкомстата России являются:
Реализация государственной политики в области гос. статистики;
Разработка и совершенствование системы статистических показателей, характеризующих состояние экономики и социальной сферы;
Разработка научно обоснованной официальной статистической методологии, соответствующей международным стандартам;
Координация деятельности федеральных органов исполнительной власти по формированию гос ресурсов в области статистики;
Разработка информационной системы гос статистики;
Обеспечение хранения и защиты информации;
Осуществление международного сотрудничества.
За рубежом
В мировой практике существует две системы организации национальных статистических служб: централизованная и децентрализованная.
В централизованной системе руководство всеми правительственными органами, осуществляющими статистическую деятельность, ведется из единого центра (Россия, Европа)
При децентрализованной системе многие государственные учреждения занимаются сбором, обработкой и публикацией статистической информации. (США, Япония)
Оба варианта организации статистики основаны на признании существования официальной и неофициальной статистики.
Официальная статистика проводит обследования на основе соответствующих общегосударственных законодательных актов. В них зафиксирована обязанность респондентов предоставить в соответствующие государственные учреждения необходимые сведения, а названных государственных органов – сохранять в тайне конфиденциальные сведения и использовать их в сугубо статистических целях.
К организациям, которые представляют неофициальную статистику относят:
1) экономические союзы и объединения
2) статистические службы или научно-исследовательские экономические институты профессиональных объединений и политических партий
3) научно-исследовательские экономические институты по изучению рынка, общественного мнения и проведению опросов
Назначение неофициальной статистики – анализ данных официальной статистики, что не исключает возможности расширения информационной базы за счет проведения собственных статистических исследований.
Билет №3
Этапы статистического исследования.
Статистической информацией называется совокупность сведений соц-эк характера, полученных в результате статистического наблюдения, на основе которых осуществляется учет и контроль, планирование, статистический анализ и управление.
Статистическое наблюдение – это научно организованный, плановый и систематический процесс сбора массовых сведений о соц-эк явлениях и процессах путем регистрации заранее намеченных существенных признаков.
Процесс проведения статистического наблюдения включает следующие этапы:
Программно-методологическая подготовка проведения наблюдения. Включает следующие виды работ: определения цели и объекта наблюдения; состава признаков, подлежащих регистрации; разработка документов для сбора данных; выбор отчетной единицы и единицы, относительно которой будет проводится наблюдение; определение методов и средств получения данных.
Организационная подготовка проведения наблюдения. Включает следующие виды работ: подбор и подготовка кадров для проведения наблюдения; составление календарного плана проведения работ по подготовке, проведению и обработке материалов статистического наблюдения.
Выбор формы, способа и вида статистического наблюдения.
Проведение статистического наблюдения, сбор данных наблюдения, накапливание статистической информации.
Синтаксический, логический и арифметический контроль данных статистического наблюдения.
Выработка выводов и предложений по проведению статистического наблюдения. Анализ точности и достоверности.
Билет №4
1.Формы, виды, способы статистического наблюдения.
Формы статистического наблюдения.
В отечественной статистике используют три организационные формы (типы) статистического наблюдения:
Отчетность (предприятий, организаций – имеет обязательный характер, юридическую силу, обладает документальной обоснованностью. Бывает ежедневной, недельной и т.д. Также – электронной, телеграфной и т.д.)
Специально организованное статистическое наблюдение (переписи, единовременные учеты)
Регистры (система, постоянно следящая за единицей наблюдения и оценивающая силу воздействия внешних факторов на изучаемые показатели).
Способы статистического наблюдения.
Непосредственное наблюдение (сами регистраторы путем непосредственного замера, взвешивания, подсчета и тд устанавливают факт, подлежащий регистрации, и на этой основе производят запись в формуляр наблюдения).
Документальное наблюдение (основано на использовании в качестве источника статистической информации различного рода документов, как правило, учетного характера).
Опрос (способ наблюдения, при котором необходимы сведения получают со слов респондента. Устный, корреспондентский, анкетный, явочный)
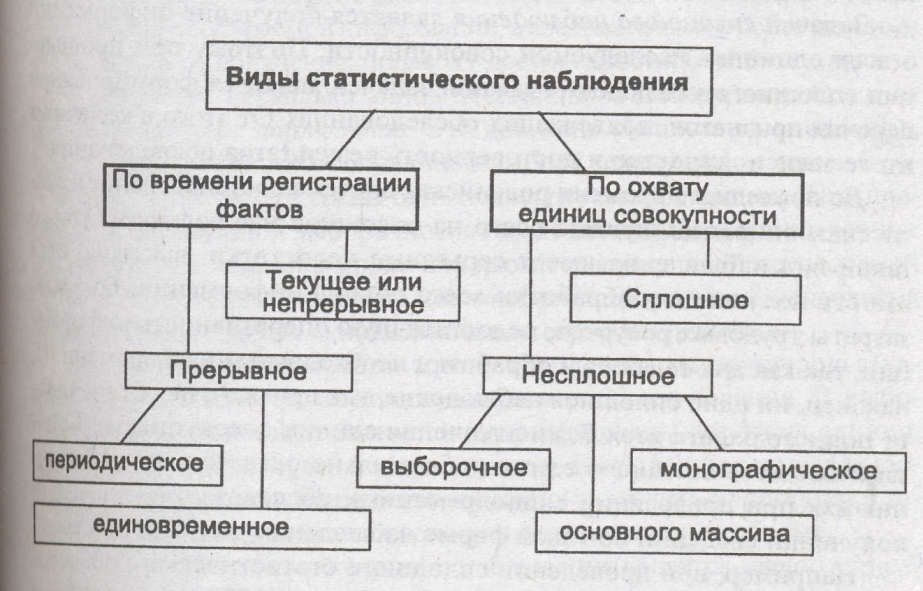
Виды статистического наблюдения.
По времени регистрации фактов (наблюдение бывает непрерывным (текущим), периодическим и единовременным).
По охвату единиц совокупности (сплошное – обо всех единицах совокупности и несплошное – выборочное (случайный отбор единиц), основного массива (самые крупные единицы исследуются), монографическое (обычно представители каких-либо типов явлений)).
Билет №5
Программно-методологические вопросы статистического наблюдения.
Цель наблюдения. Чаще всего практическая цель – получение достоверной информации для выявления закономерностей развития явлений и процессов.
Объект и единица наблюдения. Отчетная единица. При подготовке наблюдения кроме цели следует точно определить, что именно подлежит обследованию, т.е. установить объект наблюдения. Под объектом наблюдения понимается некоторая статистическая совокупность, в которой протекают исследуемые соц-эк явления и процессы.
Единицей статистики называют составной элемент объекта, являющийся носителем признаков, подлежащих регистрации.
Отчетной единицей называется субъект, от которого поступают данные о единице наблюдения.
Программа статистического наблюдения.
Необходимо отобрать те признаки, которые являются существенными, основными для характеристики объекта исходя из цели исследования.
Программа наблюдения – это перечень признаков (или вопросов), подлежащих регистрации в процессе наблюдения.
Требования к программе статистического наблюдения.
Программа должна содержать существенные признаки, непосредственно характеризующие изучаемое явление, его тип, основные черты, свойства. Вопросы программы должны быть точными и недвусмысленными, легкими для понимания. Целесообразно включить контрольный вопросы для проверки и уточнения собираемых данных. Порядок вопросов должен быть логичным.
Вопросы могут быть закрытые и открытые. Закрытый вопрос – это вопрос альтернативный (да - нет или более ответов). Открытый вопрос– можно ответить бесчисленным количеством способов.
Статистический формуляр.
Это документ единого образца, содержащий программу и результаты наблюдения.
Место и время наблюдения. Выбор места проведения зависит от цели.
Выбор времени наблюдения заключается в решении двух вопросов:
Установлении критического момента (даты) или интервала времени;
Определении срока (периода) наблюдения.
Билет №6
Сводка и группировка как этап статистического исследования.
В результате статистического наблюдения собирают сведения о каждой единице наблюдения, т.е. исходный материал. Дальнейшая задача состоит в приведении этого материала в определенный порядок. Она решается с помощью сводки.
Сводка в узком смысле слова — это подсчет итогов в группах и подгруппах и оформление этого материала в таблицы.
Сводка в широком смысле слова — это процесс, рациональной обработки данных наблюдения с целью приведения их в стройную систему, удобную для анализа и практического использования.
Основная задача сводки состоит в систематизации и обобщении результатов наблюдения таким образом, чтобы стали возможными выявление характерных черт совокупности и определение тенденции в целом.
Этапы сводки:
1) группировка полученных при наблюдении данных;
2) разработка системы показателей, характеризующих типичные группы и подгруппы изучаемой совокупности явлений;
3) подсчет итогов в группах и подгруппах;
4) оформление таблиц.
Программа сводки в общем виде содержит перечень групп, на которые нужно распределить совокупность, а также перечень показателей, используемых для характеристики совокупности в целом, ее отдельных частей.
План сводки — это этапы ее последовательности, сроки выполнения отдельных частей сводки, исполнители и порядок изложения результатов сводки.
В результате сводки получают итоги по показателям, однако этих сведений недостаточно для анализа и выявления закономерностей, поэтому необходимо выделять из общей совокупности какие-то части, группы. Эту задачу решает группировка.
Группировка — это метод, который позволяет распределить совокупность на группы по признакам сходства или различия. Одним из важнейших этапов группировки является выбор группировочного признака, потому что от этого зависят результаты сводки и группировки в целом. Выбор признаков в каждом конкретном случае должен основываться на экономической сущности изучаемого явления, на основе тщательного анализа.
С помощью метода группировки решаются следующие важнейшие задачи:
1) выделение социально-экономических типов;
2) определение структуры однотипных совокупностей;
3) выявление связи и зависимости между явлениями. Существуют несколько различных классификаций группировок.
В зависимости от задач, решаемых группировкой, выделяют:
1) типологические группировки — в их основе лежит выделение социально-экономических типов общественных явлений;
2) структурные группировки — характеризующие распределение какой-либо совокупности на группы в процентах к итогу;
3) аналитические группировки — характеризующие взаимосвязь между изучаемыми признаками.
В зависимости от количества группировочных признаков выделяют:
1) простые группировки — это распределение совокупности на группы по одному признаку;
2) комбинационные группировки — это распределение совокупности по двум-трем признакам, взятым в комбинации друг с другом, в этой группировке группы, образованные по одному признаку, разделяются на подгруппы по другому признаку.
В зависимости от характера группировочного признака различают:
1) атрибутивные группировки — в их основе лежит качественный признак, выражающийся словом;
2) количественные группировки — в их основе лежит количественный признак, выражающийся числом.
В зависимости от характера статистических данных различают:
1) первичные группировки — это группировки, построенные непосредственно на основе данных наблюдения. Эти группировки осуществляются органами статистики или предприятиями;
2) вторичные группировки — это группировки, построенные на основе данных других группировок, т.е. это образование новых групп на основе ранее проведенной группировки.
Билет №7
Виды статистических группировок.
см. билет №6
Билет №8
Правила построения статистических таблиц.
Результаты сводки и группировки материалов статистического наблюдения представляются, как правило, в виде статистических таблиц, которые должны содержать сводную качественную характеристику изучаемой совокупности по одному или нескольким существенным признакам.
Каждая таблица состоит из подлежащего и сказуемого. Подлежащее – то, о чем говорится в таблице (объект изучения); сказуемое – то, что говорится о подлежащем, его характеристика с помощью системы показателей. Подлежащее обычно располагается в левой части таблицы, сказуемое – в верхней в виде названия граф.
Таблицы бывают:
Простые (перечневые, когда подлежащее – перечень единиц, составляющих объект изучения);
Территориальные (дается перечень территорий, стран, областей. городов);
Хронологические (в подлежащем – даты)
Сложные (групповые или комбинированные).
Практикой выработаны определенные требования к составлению и оформлению таблиц:
Статистическая таблица обязательно имеет заголовок, в котором должны быть указаны цель построения таблицы, территория и время, к которым относятся данные);
Таблица по возможности должна быть краткой;
В таблице желательно давать нумерацию граф.
Приводимые в подлежащем и сказуемом признаки должны быть в логическом порядке с учетом необходимости рассматривать их совместно.
Таблица может сопровождаться примечаниями, в которых указываются источники данных, более подробно раскрывается содержание показателей.
Округленные числа в таблицах приводятся с одинаковой степенью точности.
Билет №9
Абсолютные величины: их виды, единицы измерения
Статистика изучает количественную сторону массовых явлений и процессов с помощью статистических величин, которые делятся на абсолютные и относительные величины.
Абсолютные величины характеризуют размеры в конкретных условиях времени и места. Они дают характеристику всей совокупности.
Единицы измерения абсолютных величин;
1) натуральные, отражающие природные свойства явления, — физическая мера веса, длины и др. Основной недостаток натуральных единиц измерения заключается в том, что невозможно суммирование различных натуральных абсолютных величин;
2) условно-натуральные (используются с целью суммирования разной по форме продукции потребительского назначения);
3) комбинированные. Их получают в результате перемножения или деления двух натуральных единиц измерения;
4) стоимостные (денежные). Устраняют недостатки предыдущих единиц измерения, позволяю оценить разнородную продукцию.
Однако абсолютные величины не дают всеобъемлющей характеристики исследуемых явлений и процессов и не всегда пригодны для сравнения. Это вызывает необходимость использования относительных величин, которые используются при сопоставлениях, сравнениях и исполняют роль меры соотношения.
Относительные величины — это отвлеченные статистические величины, выражающие количественное соотношение двух величин.
Билет №10. Относительные величины: формы выражения, виды и особенности применения в экономическом анализе
Относительные величины – результат сравнения между собой 2-х абсолютных величин, представляют собой частное от деления двух статистических величин и характеризуют количественное соотношение между ними.
У относительных величин особенно важная роль, так как они дают полную картину явления.
При расчете относительных величин следует иметь в виду, что в числителе всегда находится показатель, отражающий то явление, которое изучается, т.е. сравниваемый показатель, а в знаменателе — показатель, с которым производится сравнение, принимаемый за основание или базу сравнения. В зависимости от того, какое числовое значение имеет база сравнения, результат отношения может быть выражен либо в форме коэффициента или процента, либо в форме промилле и децимилле.
Если значение основания или базы сравнения принимается =1, то относительная величина является коэффициентом и показывает, во сколько раз изучаемая величина больше основания.
Если значение основания или базу сравнения =100, результат вычисления относительной величины будет выражаться в процентах.
В тех случаях, когда базу сравнения
принимают за 1000, результат сравнения
выражается в промилле
 .
.
3 необходимых параметра по регламентации ООН:
Показатель должен иметь типовые параметры развития (без резких взлетов и падений, нельзя кризисные явления или пиковые, средние показатели должны быть за несколько лет)
Показатели базисного года не должны сильно отстоять от изучаемого периода
База сравнения должна периодически меняться (строго 10/5 лет)
Способы определения относительных величин.
ОВ динамики— это отношение фактической величины показателя в отчетном периоде (у1) к фактической его величине в базисном, предшествующем периоде (у0): ОВД = Y1/Y0 х 100%. ОВД характеризуют изменение явления во времени, выявляют направление развития, измеряют интенсивность развития. Расчет относительных величин выполняется в виде темпов роста и других показателей динамики
ОВ выполнения плана- отношение фактической величины показателя (у1) к плановой его величине (уплана) того же периода: ОВВП=У1 /Уплана х 100%. ОВВП показывает степень выполнения плана в %;
ОВ выполнения планового задания- это отношение планируемой величины показателя (уплана) к фактически достигнутой величине в предшествующем периоде, т.е. в базисном (у0): ОВПЗ = Уллана/У0 х 100%. Показывает, на сколько % плановое задание выше (ниже) фактически достигнутого в базисном периоде. ОВПЗ называют плановым темпом роста;
Относительные величины структуры характеризуют состав изучаемой совокупности. Исчисляются они как отношение абсолютной величины каждого из элементов совокупности к абсолютной величине всей совокупности, т.е. как отношение части к целому, и представляют собой удельный вес части в целом.
Как правило, относительные величины структуры выражаются в процентах (база сравнения принимается за 100) или в долях (база сравнения принимается за 1). (часть целого/целое)
Относительные величины сравнения характеризуют количественное соотношение одноименных показателей, относящихся к различным объектам статистического наблюдения. (численность населения РФ 2013г/численность населения США 2013г.)
Относительные величины координации применяются для характеристики соотношения между отдельными частями статистической совокупности и показывают, во сколько раз сравниваемая часть совокупности больше или меньше части, которая принимается за основание или базу сравнения. (численность женщин/численность мужчин)
Относительные величины интенсивности показывают, насколько широко распространено изучаемое явление в той или иной среде, т.е. сколько единиц одной совокупности приходится на единицу другой совокупности. Сравнивает разноименные показатели. (Относительная величина уровня экономического развития – ВВП/ на душу населения, численность населения/на территорию)
Билет №11. Средняя величина как обобщающая характеристика совокупности. Научные принципы расчета средних величин
Большое распространение в статистике имеют средние величины. Средние величины характеризуют качественные показатели коммерческой деятельности: издержки обращения, прибыль, рентабельность и др.
Средняя величина – выражает то общее, что характерно для изучаемого явления в конкретных условиях места и времени. Назначение СВ состоит в том, чтобы представить конкретный признак совокупности одним число несмотря на количественные различия значений.
Средняя величина – обобщающая характеристика качества однородной совокупности, однотипных явлений по какому-то одному количественно варьирующемуся принципу.
Средняя - это обобщающие показатели, в которых находят выражение действия общих условий, закономерностей изучаемого явления, это один из распространенных приемов обобщений. Правильное понимание сущности средней определяет ее особую значимость в условиях рыночной экономики, когда средняя через единичное и случайное позволяет выявить общее и необходимое, выявить тенденцию закономерностей экономического развития.
Статистические средние рассчитываются на основе массовых данных правильно статистически организованного массового наблюдения (сплошного и выборочного). Однако статистическая средняя будет объективна и типична, если она рассчитывается по массовым данным для качественно однородной совокупности (массовых явлений). Например, если рассчитывать среднюю заработную плату в кооперативах и на госпредприятиях, а результат распространить на всю совокупность, то средняя фиктивна, так как рассчитана по неоднородной совокупности, и такая средняя теряет всякий смысл.
При помощи средней происходит как бы сглаживание различий в величине признака, которые возникают под действием случайных факторов у отдельных единиц наблюдения.
Например, средняя выработка продавца зависит от многих причин: квалификации, стажа, возраста, формы обслуживания, здоровья и т.д.Средняя выработка отражает общее свойство всей совокупности.
Средняя величина является отражением значений изучаемого признака, следовательно, измеряется в той же размерности, что и этот признак.
Каждая средняя величина характеризует изучаемую совокупность по какому-либо одному признаку. Чтобы получить полное и всестороннее представление об изучаемой совокупности по ряду существенных признаков, в целом необходимо располагать системой средних величин, которые могут описать явление с разных сторон.
Основные условия расчета и анализа СВ:
СВ должны подсчитываться только для качественно однородных совокупностей
В экономическом анализе СВ, как правило, дополняются отдельными индивидуальными показателями, характеризующими развитие явления/процесса – например, min/max значение признака. Это делается для того, чтобы понять насколько типична данная СВ, кроме того за ними могут быть скрыты плохие результаты работы отдельных предприятий.
Необходимо правильно выбрать форму СВ, верно определить свособь ее расчета.
Существуют различные средние:
средняя арифметическая;
средняя геометрическая;
средняя гармоническая;
средняя квадратическая;
средняя хронологическая.
Структурные средние – мода и медиана
Билет №12. Средняя арифметическая: простая и взвешенная, особенности применения
Средняя арифметическая простая (невзвешенная) равна сумме отдельных значений признака, деленной на число этих значений.
Отдельные значения признака называют
вариантами и обозначают через х (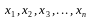 );
число единиц совокупности обозначают
через n, среднее значение признака -
через
);
число единиц совокупности обозначают
через n, среднее значение признака -
через
 .
Следовательно, средняя арифметическая
простая равна:
.
Следовательно, средняя арифметическая
простая равна:

Когда варианты признаков встречаются
неодинаковое количество раз следует
использовать формулу средней арифметической
взвешенной:
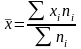 ,
,
где
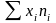 — фактически выпущенная продукция,
получаемая путём умножения вариант
(процент выполнения плана) на веса
(выпуск продукции по плану).
— фактически выпущенная продукция,
получаемая путём умножения вариант
(процент выполнения плана) на веса
(выпуск продукции по плану).
Производя вычисления, варианты (х) лучше брать в коэффициентах.
Средняя простая – частный случай средней взвешенной.
В отличие от средней арифметической простой, величина средней арифметичской взвешенной зависит не только от размера значений признака, но и от величин соответствующих им частот. Причем по своему цифровому значению СВ будет ближе к варианту с наибольшей частотой.
Основные свойства средней арифметической.
Средняя арифметическая обладает рядом свойств:
1. Если все частоты разделить или умножить на какое-либо число, то величина средней НЕ изменится.
2. Общий множитель индивидуальных значений признака может быть вынесен за знак средней:
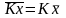
То есть если каждый вариант умножить/разделить на какое-то постоянное число, то и СВ уменьшится/увеличится во столько же раз
3. Если от каждого варианта вычесть или прибавить к каждому постоянное число, то СВ уменьшится/увеличится на это число.
3. Средняя суммы (разности) двух или нескольких величин равна сумме (разности) их средних:
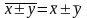
5. Сумма отклонений значений признака Х от средней арифметической х равна нулю:
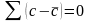
Билет №13. Средняя гармоническая: простая и взвешенная, особенности применения
Наряду со средней арифметической, в статистике применяется средняя гармоническая величина, обратная средней арифметической из обратных значений признака. Как и средняя арифметическая, она может быть простой и взвешенной.
Ср.гармон.простая:
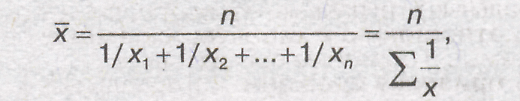 где
n—число единиц совокупности
или число вариантов; х —значения
варьирующегося признака; показатель
степени=(-1). Используется для
несгруппированных данных. Взаимосвязана
с ср.ар.простой как величина,обратная
ср.ар., рассчитанная из обратных значений
признака. Нужна, если согласно исходному
соотношению средней надо,чтобы в
знаменателе располагались обратные
знач. осредняемого признака.+если
значения признаков-весов одинаковы,=>образуется
тождество между ср.гармон.взвеш. и
ср.гармон.простой.
где
n—число единиц совокупности
или число вариантов; х —значения
варьирующегося признака; показатель
степени=(-1). Используется для
несгруппированных данных. Взаимосвязана
с ср.ар.простой как величина,обратная
ср.ар., рассчитанная из обратных значений
признака. Нужна, если согласно исходному
соотношению средней надо,чтобы в
знаменателе располагались обратные
знач. осредняемого признака.+если
значения признаков-весов одинаковы,=>образуется
тождество между ср.гармон.взвеш. и
ср.гармон.простой.
Средняя гармоническая взвешенная
строится по формуле:
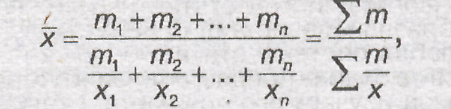 Где
х – значения варьирующего признака; m
– значения сводного, объемного показателя,
выступающего как признак-вес; Рассчитывается
если имеющиеся данные предоставляют
сведения об объеме определяющего
показателя,рассчитываемого как
произведение осредняемого признака и
признака-веса+ если есть сведения об
индивидуальных знач. осредняемого
признака, а данных об отдельных знач.
признака-веса нет. Применяют когда надо
рассчитать общую среднюю из групповых
ср.величин; среднюю относительную
величину, если неизвестна величина в
знаменателе осредняемого признака.
Где
х – значения варьирующего признака; m
– значения сводного, объемного показателя,
выступающего как признак-вес; Рассчитывается
если имеющиеся данные предоставляют
сведения об объеме определяющего
показателя,рассчитываемого как
произведение осредняемого признака и
признака-веса+ если есть сведения об
индивидуальных знач. осредняемого
признака, а данных об отдельных знач.
признака-веса нет. Применяют когда надо
рассчитать общую среднюю из групповых
ср.величин; среднюю относительную
величину, если неизвестна величина в
знаменателе осредняемого признака.
Выводы:
В средней гармонической статистическим весом являеются не прямые частоты признака, а их произведение на величину (w=x*f)
Вместо средней гармонической можно рассчитать среднее арифметическое, сделав заранее сумму частот (размер частот)
Билет № 14. Показатели отклонений от средней величины: методика расчета и особенности применения
Показатели вариации.
Различие индивидуальных значений признака внутри изучаемой совокупности в статистике называется вариацией признака.
Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов, которые по-разному сочетаются в каждом отдельном случае.
Средняя величина — это абстрактная, обобщающая характеристика признака изучаемой совокупности, но она не показывает строения совокупности, которое весьма существенно для ее познания. Средняя величина не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они вблизи или значительно отклоняются от нее. В некоторых случаях отдельные значения признака близко примыкают к средней арифметической и мало от нее отличаются. В таких случаях средняя хорошо представляет всю совокупность.
В других, наоборот, отдельные значения совокупности далеко отстают от средней, и средняя плохо представляет всю совокупность.
Колеблемость отдельных значений характеризуют показатели вариации.
Термин "вариация" произошел от латинского variatio –“изменение, колеблемость, различие”. Однако не всякие различия принято называть вариацией. Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием действия различных факторов. Различают вариацию признака: случайную и систематическую.
Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих ее факторов. Например, изучая силу и характер вариации в выделяемой совокупности, можно оценить, насколько однородной является данная совокупность в количественном, а иногда и качественном отношении, а следовательно, насколько характерной является исчисленная средняя величина. Степень близости данных отдельных единиц хi к средней измеряется рядом абсолютных, средних и относительных показателей.
Абсолютные и средние показатели вариации и способы их расчета.
Для характеристики совокупностей и исчисленных величин важно знать, какая вариация изучаемого признака скрывается за средним. Для характеристики колеблемости признака используется ряд показателей. Наиболее простой из них - размах вариации.
Размах вариации - это разность между
наибольшим ( )
и наименьшим (
)
и наименьшим ( )
значениями вариантов.
)
значениями вариантов.
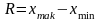
Этот показатель улавливает только крайние отклонения и не отражает отклонений всех вариант в ряду.
Чтобы дать обобщающую характеристику распределению отклонений, исчисляют среднее линейное отклонение d, которое учитывает различие всех единиц изучаемой совокупности.
Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учета знака этих отклонений:
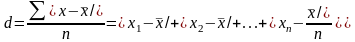 .
.
Порядок расчета среднего линейного отклонения следующий:
1) по значениям признака исчисляется средняя арифметическая:
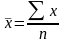 ;
;
2) определяются отклонения каждой
варианты
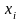 от средней
от средней
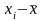 ;
;
3) рассчитывается сумма абсолютных
величин отклонений:
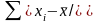 ;
;
4) сумма абсолютных величин отклонений делится на число значений:
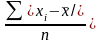 .
.
Если данные наблюдения представлены в виде дискретного ряда распределения с частотами, среднее линейное отклонение исчисляется по формуле средней арифметической взвешенной:
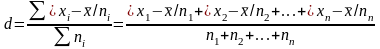
Порядок расчета среднего линейного отклонения взвешенного следующий:
1) вычисляется средняя арифметическая взвешенная:
 ;
;
2) определяются абсолютные отклонения вариант от средней / /;
3) полученные отклонения умножаются на
частоты
 ;
;
4) находится сумма взвешенных отклонений без учета знака:
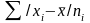 ;
;
5) сумма взвешенных отклонений делится на сумму частот:
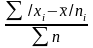 .
.
Расчет дисперсии и среднего квадратического отклонения по индивидуальным данным и в рядах распределения.
Основными обобщающими показателями вариации в статистике являются дисперсии и среднее квадратическое отклонение.
Дисперсия - это средняя арифметическая
квадратов отклонений каждого значения
признака от общей средней. Дисперсия
обычно называется средним квадратом
отклонений и обозначается
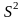 .
В зависимости от исходных данных
дисперсия может вычисляться по средней
арифметической простой или взвешенной:
.
В зависимости от исходных данных
дисперсия может вычисляться по средней
арифметической простой или взвешенной:
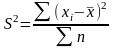 — дисперсия невзвешенная (простая);
— дисперсия невзвешенная (простая);
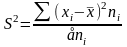 — дисперсия взвешенная.
— дисперсия взвешенная.
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается S:
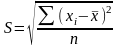 — среднее квадратическое отклонение
невзвешенное;
— среднее квадратическое отклонение
невзвешенное;
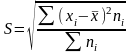 — среднее квадратическое отклонение
взвешенное.
— среднее квадратическое отклонение
взвешенное.
Среднее квадратическое отклонение - это обобщающая характеристика абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.).
Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупность.
Вычислению среднего квадратического отклонения предшествует расчет дисперсии.
Порядок расчета дисперсии взвешенную:
1) определяют среднюю арифметическую взвешенную
;
2) определяются отклонения вариант от
средней
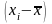 ;
;
3) возводят в квадрат отклонение каждой
варианты от средней
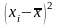 ;
;
4) умножают квадраты отклонений на веса
(частоты)
 ;
;
5) суммируют полученные произведения
 ;
;
6) Полученную сумму делят на сумму весов
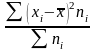 .
.
Расчет дисперсии по формуле
 по индивидуальным данным и в рядах
распределения.
по индивидуальным данным и в рядах
распределения.
Техника вычисления дисперсии сложна, а при больших значениях вариант и частот может быть громоздкой. Расчеты можно упростить, используя свойства дисперсии.
Свойства дисперсии.
Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсии не изменяет.
Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсии не изменяет.
Уменьшение или увеличение каждого значения признака в какое-то число раз к соответственно уменьшает или увеличивает дисперсию в
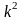 раз, а среднее квадратическое отклонение
- в к раз.
раз, а среднее квадратическое отклонение
- в к раз.Дисперсия признака относительно произвольной величины всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной:
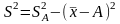 .
Если А равна нулю, то приходим к
следующему равенству:
,
т.е. дисперсия признака равна разности
между средним квадратом значений
признака и квадратом средней.
.
Если А равна нулю, то приходим к
следующему равенству:
,
т.е. дисперсия признака равна разности
между средним квадратом значений
признака и квадратом средней.
Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими.
Порядок расчета дисперсии простой:
1) определяют среднюю арифметическую ;
2) возводят в квадрат среднюю арифметическую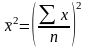 ;
;
3) возводят в квадрат каждую варианту
ряда
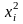 ;
;
4) находим сумму квадратов вариант
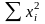 ;
;
5) делят сумму квадратов вариант на их
число, т.е. определяют средний квадрат
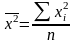 ;
;
6) определяют разность между средним
квадратом признака и квадратом средней
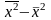 .
.
Рассмотрим расчет дисперсии в интервальном ряду распределения.
Порядок расчета дисперсии взвешенной (по формуле ):
определяют среднюю арифметическую
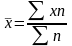 ;
;возводят в квадрат полученную среднюю
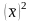 ;
;возводят в квадрат каждую варианту ряда ;
умножают квадраты вариант на частоты
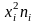 ;
;суммируют полученные произведения
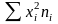 ;
;делят полученную сумму на сумму весов и получают средний квадрат признака
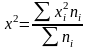 ;
;определяют разность между средним значением квадратов и квадратом средней арифметической, т.е. дисперсию .
Средняя величина отражает тенденцию развития, т.е. действие главных причин. Среднее квадратическое отклонение измеряет силу воздействия прочих факторов.
Показатели относительного рассеивания.
Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.
Коэффициент вариации.
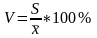
Билет № 15. Виды динамических рядом и правила их построения
Основная цель статистического изучения динамики коммерческой деятельности состоит в выявлении и измерении закономерностей их развития во времени. Это достигается посредством построения и анализа статистических рядов динамики.
Рядами динамики называются статистические данные, отображающие развитие изучаемого явления во времени. В каждом ряду динамики имеются два основных элемента: показатель времени t; соответствующие им уровни развития изучаемого явления у. В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты) времени, либо отдельные периоды (годы, кварталы, месяцы, сутки).
Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.
В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим, ряды динамики подразделяются на моментные и интервальные.
Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени.
Примером моментного ряда динамики является следующая информация о списочной численности работников фирмы N в 1994 г.:
Дата |
1.01 |
1.04 |
1.07 |
1.10 |
1.01 |
Год |
1994 г. |
1994 г. |
1994 г. |
1994 г. |
1995 г. |
Число работников, чел. |
192 |
190 |
195 |
198 |
200
|
Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности. Так, основная часть персонала фирмы N, составляющая списочную численность на 1.01.1994г., продолжающая работать в течение данного года, отображена в уровнях последующих периодов. Поэтому при суммировании уровней моментного ряда динамики может возникнуть повторный счет.
Интервальные ряды динамики отображают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.
Примером интервального ряда динамики могут служить данные о розничном товарообороте магазина в 1990-1994 гг.:
Год |
1990 |
1991 |
1992 |
1993 |
1994 |
Объем розничного товарооборота, тыс. руб. |
885,7 |
932,6 |
980,1 |
1028,7 |
1088,4 |
Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы времени. Например, суммируя товарооборот за первые три месяца года, получают его объем за I квартал, а сумма товарооборота четырех кварталов дает объем товарооборота за год и т.д.
Ряды динамики могут быть полными и неполными.
Полный ряд - ряд динамики, в котором одноименные моменты времени или периоды времени строго следуют один за другим в календарном порядке или равноотстоят друг от друга.
Неполный ряд динамики - ряд, в котором уровни зафиксированы в неравноотстоящие моменты или периоды времени.
Приведение рядов динамики в сопоставимый вид.
Ряды динамики, изучающие изменение статистического показателя, могут охватывать значительный период времени, на протяжении которого могут происходить события, нарушающие сопоставимость отдельных уровней ряда динамики (изменение методологии учета, изменение цен и т.д.).
Для того, чтобы анализ ряда был объективен, необходимо учитывать события, приводящие к несопоставимости уровней ряда и использовать приемы обработки рядов для приведения их в сопоставимый вид.
Наиболее характерные случаи несопоставимости уровней ряда динамики:
Территориальные изменения объекта исследования, к которому относится изучаемый показатель (изменение границ городского района, пересмотр административного деления области и т.д.).
Разновеликие интервалы времени, к которым относится показатель. Так, например, в феврале - 28 дней, в марте - 31 день, анализируя изменения показателя по месяцам, необходимо учитывать разницу в количестве дней.
Изменение даты учета. Например, численность поголовья скота в разные годы могла определяться по состоянию на 1 января или на 1 октября, что в данном случае приводит к несопоставимости.
Изменение методологии учета или расчета показателя.
Изменение цен.
Изменение единиц измерения.
Основные правила построения динамических рядов:
Все показатели динамического ряда должны относиться к равнозначным периодам времени (очевидно, что данные за год и за квартал несопоставимы)
Показатели динамического ряда должны быть однородны по составу, то есть иметь одну и ту же полноту охвата объектов наблюдения
Показатели должны быть рассчитаны по единой методологии
При построении ряда динамики должны соблюдаться последовательность и непрерывность ряда (в случае разрыва ряда динамики, то есть отсутствия данных за определенный период(или на определенный момент), часто прибгают к приблизительному расчету этих показателей методами интерполяции и экстраполяции.
С точки зрения экономического анализа ряд динамики делится на 3 уровня : начальный, средний, конечный. Если начальный и конечный определяются местоположением показателя в динамическом ряде (первый и последний), то средний является величиной расчетной. Средний уровень принято называть средней хронологической.
Билет № 16. Средняя хронологическая: ее значение, методики расчета
В качестве обобщенной характеристики
уровней ряда динамики служит средний
уровень ряда динамики
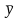 .
В зависимости от типа ряда динамики
используются различные расчетные
формулы.
.
В зависимости от типа ряда динамики
используются различные расчетные
формулы.
Интервальный ряд абсолютных величин с равными периодами (интервалами времени):

Моментный ряд с равными интервалами между датами:
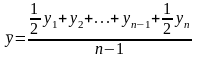
Моментный ряд с неравными интервалами между датами:
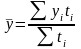
где
 - уровни ряда, сохраняющиеся без
изменения на протяжении интервала
времени
- уровни ряда, сохраняющиеся без
изменения на протяжении интервала
времени
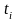 .
.
Билет № 17. Производные абсолютные показатели динамического ряда
Анализ скорости и интенсивности развития явления во времени осуществляется с помощью аналитических показателей, которые получаются в результате сравнения уровней РД между собой. К абсолютным аналитическим показателям относят абсолютный прирост, абсолютное значение 1% прироста. Принято сравниваемый уровень называть отчетным, а уровень, с которым сравнивают, - базисным.
Абсолютный прирост - разность между двумя уровнями ряда динамики, имеет ту же размерность, что и уровни самого ряда динамики. Абсолютные приросты могут быть цепными и базисными, в зависимости от способа выбора базы для сравнения:
цепной абсолютный прирост -
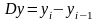 ;
;
базисный абсолютный прирост -
 .
.
Для относительной оценки абсолютных приростов рассчитываются показатели темпов прироста.
По показателям изменения уровней ряда динамики (абсолютные приросты, темпы роста и прироста), полученным в результате анализа исходного ряда, могут быть рассчитаны обобщающие показатели в виде средних величин - средний абсолютный прирост, средний темп роста, средний темп прироста.
Абс знач 1% прироста.- представляет
собой 1\100 часть базисного уровня+
отношение абсолютного прироста к
соответствующему темпу прироста:
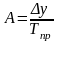 ,
где А- обозначение абс. знач. 1%
прироста.Служит косвенной мерой базисного
уровня и вместе с темпом прироста
позволяет рассчитать абс прирост уровня
за рассматриваемый период, т.е. показывает,
сколько абсолютных единиц приходится
на 1% прироста.
,
где А- обозначение абс. знач. 1%
прироста.Служит косвенной мерой базисного
уровня и вместе с темпом прироста
позволяет рассчитать абс прирост уровня
за рассматриваемый период, т.е. показывает,
сколько абсолютных единиц приходится
на 1% прироста.
Билет № 18. Производные относительные показатели динамического ряда
Для оценки эффективности изменения уровня ДР используют относительные показатели динамики: коэффициент роста, выраженный в долях единицы; темп роста в %.
Темп роста - относительный показатель,
получающийся в результате деления двух
уровней одного ряда друг на друга.
Темпы роста могут рассчитываться как
цепные, когда каждый уровень ряда
сопоставляется с предшествующим ему
уровнем:
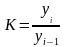 ,
либо как базисные, когда все уровни
ряда сопоставляются с одним и тем же
уровнем
,
либо как базисные, когда все уровни
ряда сопоставляются с одним и тем же
уровнем
 ,
выбранным за базу сравнения:
,
выбранным за базу сравнения: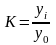 . Темпы роста могут быть представлены
в виде коэффициентов либо в виде
процентов.
. Темпы роста могут быть представлены
в виде коэффициентов либо в виде
процентов.
Темп прироста - относительный показатель, показывающий на сколько процентов один уровень ряда динамики больше (или меньше) другого, принимаемого за базу для сравнения. Темп прироста показывает, на сколько % изменилась величина уровня ДР за изучаемый период времени.
Базисные темпы прироста:
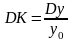
 .
.
Цепные темпы прироста:
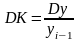 .
.
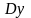 и
и
 -
абсолютный базисный или цепной прирост;
-
абсолютный базисный или цепной прирост;
- уровень ряда динамики, выбранный за базу для определения базисных абсолютных приростов;
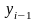 - уровень ряда динамики, выбранный за
базу для определения i-го цепного
абсолютного прироста.
- уровень ряда динамики, выбранный за
базу для определения i-го цепного
абсолютного прироста.
Существует связь между темпами роста и прироста:
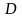 К
= К - 1 или
К
= К - 100 % (если темпы роста определены в
процентах).
К
= К - 1 или
К
= К - 100 % (если темпы роста определены в
процентах).
Если разделить абсолютный прирост
(цепной) на темп прироста (цепной) за
соответствующий период, получим
показатель, называемый - абсолютное
значение одного процента прироста:
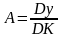 .
.
Средний темп роста можно определить, пользуясь формулами:
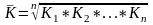
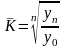
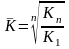
где n - число рассчитанных цепных или базисных темпов роста;
- уровень ряда, принятый за базу для сравнения;
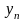 - последний уровень ряда;
- последний уровень ряда;
 - цепные темпы роста (в коэффициентах);
- цепные темпы роста (в коэффициентах);
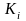 -
первый базисный темп роста;
-
первый базисный темп роста;
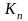 -
последний базисный темп роста.
-
последний базисный темп роста.
Между темпами прироста
 и темпами роста К существует соотношение
=
К - 1, аналогичное соотношение верно и
для средних величин.
и темпами роста К существует соотношение
=
К - 1, аналогичное соотношение верно и
для средних величин.
Коэфф роста Кр определяют по формулам:
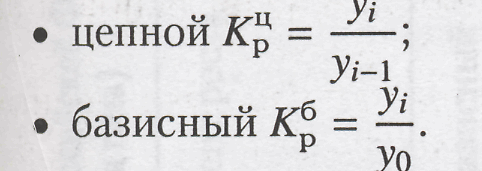
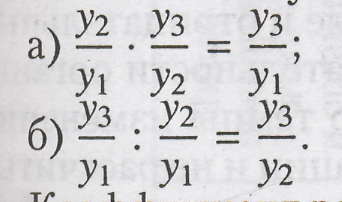 Взаимосвязь
цепных и базисных коэффроста: а)
произведение цепных коэффиц роста=
базисному коэффиц роста за весь период.
б) частное от деления последующего
базисного коэффиц роста на предыдущий=
соответствующему цепному коэффиц
роста.
Взаимосвязь
цепных и базисных коэффроста: а)
произведение цепных коэффиц роста=
базисному коэффиц роста за весь период.
б) частное от деления последующего
базисного коэффиц роста на предыдущий=
соответствующему цепному коэффиц
роста.
Коэффициент роста показывает, во сколько раз увеличился уровень ДР по сравн с базисным, а в случае уменьшения— какую часть базисного составляет сравниваемый уровень. Темпы и коэффиц роста отличаются только единицами измерения. Формулы расчета темпов роста следующие:
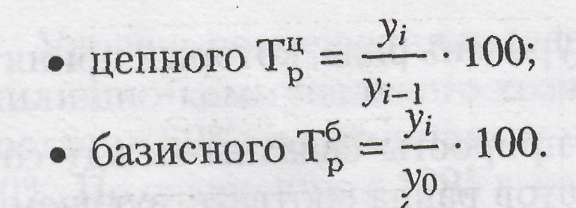
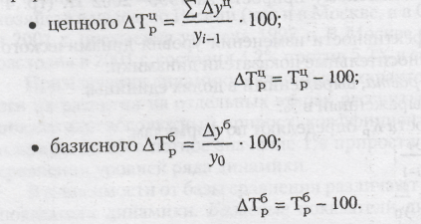 Темпы
прироста (сокращения) так же, как и темпы
роста, исчисляют по годам (цепным методом)
и накопленным итогом за длительный
период (базисным методом).
Темпы
прироста (сокращения) так же, как и темпы
роста, исчисляют по годам (цепным методом)
и накопленным итогом за длительный
период (базисным методом).
Билет №19
Среднегодовые показатели роста и прироста (абсолютные и относительные).
Для характеристики динамики изучаемого явления за продолжительный период рассчитывают группу средних показателей динамики. 2 категории показателей: а)средние уровни ряда;
б)средние показатели изменения уровней ряда.
А) Средние уровни ряда рассчитываются в зависимости от вида временного ряда.
1. Для интервальных
РД абсолютных показателей средний
уровень ряда рассчитывается по формуле
простой средней арифметической:
 где n - число уровней ряда.
где n - число уровней ряда.
2. а) Средний уровень моментного
ряда с
равными интервалами
рассчитыв по формуле средней
хронологической:
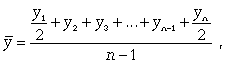 где n - число дат.
где n - число дат.
2. б) Средний уровень моментного
ряда с неравными интервалами
рассчитывается по формуле ср ар
взвешенной:
![]()
Б) Средние показатели изменения уровней ряда:
1. Средний
абсолютный прирост (ср
скорость роста) определяется как средняя
арифметическая из показателей скорости
роста за отдельные периоды времени:
![]()
![]() где
где
yn - конечный уровень ряда;
y1 - начальный уровень ряда.
2. Средний коэффициент роста
(![]() )
по формуле средней геометрической из
показателей коэффициентов роста за
отдельные периоды:
)
по формуле средней геометрической из
показателей коэффициентов роста за
отдельные периоды:![]() где
где
Кр1 , Кр2 , ..., Кр n-1 - коэффициенты роста по сравнению с предыдущим периодом;
n - число уровней ряда.
Средний коэффициент роста
можно определить иначе:![]()
3. Средний темп роста-
это средний коэффициент роста, кторый
выражается в %:![]()
4. Средний темп прироста Тпр, %. Для расчета данного показателя первоначально определяется средний темп роста Тр, который затем уменьшается на 100%.
Также можно определить этот
показатель, уменьшив средний коэффициент
роста на единицу:![]()
5. Среднее абсолютное значение
1% прироста: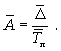
Билет №20
Способы обработки динамических рядов.
РД- значения статистических показателей, которые представлены в определенной хронологической последовательности. Каждый ДР содержит 2 составляющие: 1)показатели периодов времени; 2)показатели, характеризующие исследуемый объект за временные периоды, которые называют уровнями ряда. В зависимости от отражения динамики:
-Динамический интервальный ряд содержит значения показателей за определенные периоды времени.
- Динамический моментный ряд отражает значения показателей на определенный момент времени(дату #на первое января каждого года данные о нац богатстве).
3 основных способа обработки ДР:
а)укрупнение интервалов ДР и расчет средних для каждого укрупненного интервала; б)метод скользящей средней;
в)метод аналитич выравнивания
1) Укрупнение интервалов - наиболее простой, заключавшийся в преобразовании первоначальных РД в более крупные по продолжительности времени, что позволяет более четко выявить действие основной тенденции изменения уровней. По интервальным рядам итоги исчисляются простым суммированием уровней первоначальных рядов. Для других случаев расcчитывают СВ укрупненных рядов (переменная средняя). Переменная средняя рассчитывается по формулам простой средней арифметической.
2) Скользящая
средняя- это такая
средняя, которая последовательно
рассчитывается при передвижении на 1
интервал при заданной продолжительности
периода. Первую рассчитанную центрированную
относят ко второму периоду, 2 - к 3, 3 - к 4
ит.д. #Если продолжит периода=3, то
скользящие средние рассчитываются:![]()
![]()
3) Метод аналит выравнивания заключается в построении аналитической функции, характеризующая зависимость уровней ряда от времени.
Суть: эмпирические уровни заменяются уровнями, рассчитанными на основе определенной кривой, уравнение которой рассматривается как функция времени, вид уравнения зависит от конкретного хар-ра динамики развития.
Пр #линейная зависимость выражается формулой F(t)=a+bt -это если уровни исходного ряда изменяются с достаточно постоянной абсолютной скоростью, т.е. цепные абсолютные приросты примерно одинаковы, т.е. мат выражение тенденции- прямая линия. Если цепные абсолютные приросты более или менее равномерно увеличиваются или уменьшаются, то используют параболу: y=a+bt+ct2 Задача аналитического выравнивания состоит также в определении недостающих значений, как внутри периода так и за пределами. Способ определения неизвестных значений внутри ДР- интерполяция. Методы определения неизвестных значений:
-полусумма уравнений, расположенных рядом с интреполируемыми
-по среднему абсолютному приросту
-по темпу роста.
Экстраполяция – сп-б определения количественных значений за пределами ряда. Используется для прогнозирования факторов способных влиять на развитие явлений в будущем. Можно по среднему темпу роста, среднему абсолютному приросту, средней арифметической.
Билет №21
Интерполяция и экстраполяция в динамических рядах.
Исследование динамики социально-экономических явлений создает базу для прогнозирования, т.е. для определения ориентированных размеров уровней явления в будущем.
Задача аналитического выравнивания состоит также в определении недостающих значений как внутри периода, так и на его пределами.
Интерполяция: способ определения неизвестных значений внутри динамического ряда .
Возможные методы определения неизвестных значений:
- полусумма уровней, расположенных рядом с интерполируемыми;
-определение по среднему абсолютному приросту;
-определение по темпу роста
1) Ср.арифм. 2х соседних уровней.
Y2000 = (Y2001 + Y1999)/2
2) Среднегодовой абсолютный прирост.
Δy=(Y2012 -Y2008)/5
а) Y2009 = Y2008 + Δy
б) Y2009 = Y 2010 – Δy
Среднее число от а) и б)
3) Среднегодовой коэффициент роста.
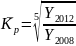
а) Y2009 = Y2008 * Kp
б) Y2009 = Y 2010 / Kp
Среднее число из а) и б)
Экстраполяция: способ определения количественных значений за пределами ряда.
Экстраполирование используется для прогнозирования факторов, способных влиять на развитие явления в будущем.
Некоторые экстраполяции и интерполяции связаны с определением неизвестных уровней динамического ряда.
Δy=(Y2012 -Y2008)/5
1) Y2013 = Y2012 + Δy
2) Y2013 = Y2012 * Kp
Билет №22
Значение экономических индексов и их классификация.
Индекс – особый статистический относительный показатель, характеризующий соотношение во времени или пространстве различных социально-экономических явлений.
Например:
Ip
=
 -
агрегатный индекс цен с весами текущего
периода (формула Пааше);
-
агрегатный индекс цен с весами текущего
периода (формула Пааше);
Iq
=
 - агрегатный индекс физического объема
с весами базисного (предыдущего) периода
(формула Ласпейреса).
- агрегатный индекс физического объема
с весами базисного (предыдущего) периода
(формула Ласпейреса).
Классификация индексов:
1) по степени охвата
По степени охвата различают индивидуальные, сводные (общие) и групповые индексы.
А) Индивидуальные индексы служат для характеристики изменения отдельных элементов сложного явления, например изменения объема производства отдельных видов продукции.
Б) Сводные индексы рассчитываются для измерения динамики сложного явления, составные части которого непосредственно несоизмеримы, например изменения физического объема продукции, включающей разноименные товары.
В) Групповые индексы охватывают не все элементы сложного явления, а только часть их, например физический объем продукции по отдельным отраслям промышленности. Групповые индексы отражают закономерности в развитии отдельных частей изучаемых явлений.
2) по базе сравнения
По базе сравнения все индексы делятся на динамические и территориальные.
А) Динамические индексы отражают изменение явления во времени. Например, индекс цен на продукцию в 2007г. по сравнению с предыдущим годом. При исчислении динамических индексов происходит сравнение значения показателя в отчетный период со значением этого же показателя за предыдущий (базисный) период. Динамические индексы, как и ряды динамики, бывают базисными и цепными.
Базисные динамические индексы –
результат сравнения текущих уровней с
одним фиксированным уровнем, принятым
за базу. Например, Iq =
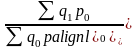 ;
I’q =
;
I’q =
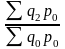 ;
;
I’’q =
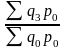 - базисные индексы Ласпейреса.
- базисные индексы Ласпейреса.
Цепные динамические индексы – результат
сравнения текущих уровней с непосредственно
предшествующими. Например, Ip =
;
I’p =
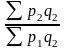 ;
;
I’’p =
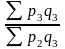 - цепные индексы Пааше.
- цепные индексы Пааше.
Б) Территориальные индексы применяются для межрегиональных сравнений. Эти индексы имеют большое значение в международной статистике при сопоставлении показателей социально-экономического развития разных стран. Например, индекс цен на автомобили в США по сравнению с Японией.
3) по виду весов:
Вес индекса – величина постоянная, одинаковая в числителе и знаменателе, служит для соизмерения индексируемых величин. По виду весов индексы бывают с постоянными и переменными весами.
А) Постоянный вес – вес базисного периода. С постоянными весами рассчитываются индексы физического объема продукции (индекс Ласпейреса, где p0 – постоянный вес).
Б) Переменный вес – вес текущего периода. С переменными весами рассчитываются индексы цен (индекс Пааше, где q1 – переменный вес).
4) В зависимости от формы построения:
В зависимости от формы построения различаются индексы агрегатные и средние.
А) Агрегатный индекс – сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов. Числитель и знаменатель агрегатного индекса представляют собой сумму произведений двух величин, одна из которых меняется (индексируемая величина – признак, изменение которого изучается), а другая остается неизменной в числителе и знаменателе (вес индекса). Агрегатные индексы – основная форма общих индексов.
Пример: Ip = - агрегатный индекс цен с весами текущего периода (формула Пааше).
Б) Средние индексы – производные, они получаются в результате преобразования агрегатных индексов, а следовательно, тождественны им. Средний индекс вычисляется как средняя величина из индивидуальных индексов. Средние индексы делятся на арифметические и гармонические.
a) Средний арифметический индекс тождествен агрегатному индексу, только если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса.
Например, Iq =
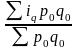 - средний арифметический индекс
физического объема продукции, где весом
является стоимость продукции базисного
периода, также как и в формуле Iq
=
.
Так как iq
- средний арифметический индекс
физического объема продукции, где весом
является стоимость продукции базисного
периода, также как и в формуле Iq
=
.
Так как iq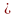 q0
= q1, то обе формулы могут быть
преобразованы друг в друга.
q0
= q1, то обе формулы могут быть
преобразованы друг в друга.
b) Средний гармонический индекс тождествен агрегатному, если индивидуальные индексы взвешены с помощью слагаемых числителя агрегатного индекса.
Например, Ip =
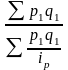 - средний гармонический индекс цен, где
весом является стоимость продукции
текущего периода, также как и в формуле
Ip =
.
- средний гармонический индекс цен, где
весом является стоимость продукции
текущего периода, также как и в формуле
Ip =
.
Так как
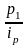 =
p0, то обе формулы могут быть
преобразованы друг в друга.
=
p0, то обе формулы могут быть
преобразованы друг в друга.
5) по характеру объекта исследования
По характеру объекта исследования общие индексы подразделяются на индексы количественных и качественных показателей. В основе такого деления лежит вид индексируемой величины. К первой группе, например, относятся индексы объема продаж долларов США на ММВБ, а ко второй – индекс курса немецкой марки.
6) по объекту исследования
по объекту исследования индексы бывают: производительности труда, себестоимости, физического объема продукции, стоимости продукции и т.д.
7) по составу явления
По составу явления можно выделить две группы индексов: постоянного (фиксированного) состава и переменного состава.
А) Индексом переменного состава называется индекс, выражающий соотношение средних уровней изучаемого явления, относящихся к разным периодам времени. Индекс переменного состава отражает изменение не только индексируемой величины, но и структуры совокупности (весов).
Например: Iпс =
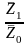 =
=
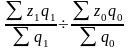 -
индекс переменного состава себестоимости
продукции.
-
индекс переменного состава себестоимости
продукции.
Б) Индекс постоянного состава – индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Индекс фиксируемого состава определяется как агрегатный индекс.
Например: Iфс =
 =
=
 -
индекс фиксированного состава
себестоимости продукции.
-
индекс фиксированного состава
себестоимости продукции.
8) по периоду исчисления
По периоду исчисления индексы подразделяются на годовые, квартальные, месячные, недельные.
Билет №23
Индивидуальные индексы стоимости (товарооборота), цен, физического объема.
Индивидуальные индексы получают в результате сравнения однотоварных явлений. Например, индекс цен на растительное масло определяется как отношение цены на этот товар в текущем периоде к цене базисного периода.
В зависимости от экономического значения индивидуальные индексы бывают физического объема продукции, цен, товарооборота и т.д.
1) Индивидуальный индекс физического объема продукции
Индивидуальный индекс физического
объема продукции iq рассчитывается
по формуле: iq =
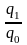 ,
где q1 – физический объем данного
товара в текущем периоде, а q0 –
физический объем данного товара в
базисном периоде.
,
где q1 – физический объем данного
товара в текущем периоде, а q0 –
физический объем данного товара в
базисном периоде.
Этот индекс показывает, во сколько раз возрос (уменьшился) выпуск какого-либо одного товара в отчетном периоде по сравнению с базисным, или сколько процентов составляет рост (снижение) выпуска товара. Если из значения индекса, выраженного в процентах, вычесть 100%, то полученная величина покажет, на сколько процентов возрос (уменьшился) выпуск продукции.
2) Индивидуальный индекс цен
Индивидуальный индекс цен ip
рассчитывается по формуле ip =
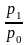 ,
где p1 – цена на данный товар в
текущем периоде, а p0 – цена на
данный товар в базисном периоде. Таким
образом, этот индекс характеризует
изменение цены одного определенного
товара в текущем периоде по сравнению
с базисным.
,
где p1 – цена на данный товар в
текущем периоде, а p0 – цена на
данный товар в базисном периоде. Таким
образом, этот индекс характеризует
изменение цены одного определенного
товара в текущем периоде по сравнению
с базисным.
3) Индивидуальный индекс стоимости продукции
Стоимость продукции – это произведение количества продукции в натуральном выражении (q) на ее цену (p).
Индивидуальный индекс стоимости продукции ipq рассчитывается по формуле
ipq =
 ,
где p1q1 – стоимость данного
товара в текущем периоде, а p0q0
– стоимость данного товара в базисном
периоде.
,
где p1q1 – стоимость данного
товара в текущем периоде, а p0q0
– стоимость данного товара в базисном
периоде.
Этот индекс отражает, во сколько раз изменилась стоимость какого-либо товара в текущем периоде по сравнению с базисным или сколько процентов составляет рост (снижение) стоимости товара.
При этом: ip iq = ipq
Пример № 1
Имеются следующие данные об объеме продаж картофеля на муниципальном рынке в одном из городов страны:
Товар |
Продано (кг) |
Средняя цена за 1кг(руб.) |
|||
Базисный период |
Отчетный период |
Базисный период |
Отчетный период |
||
Картофель |
20000 |
25000 |
20 |
30 |
|
Вычислить индивидуальные индексы цены, физического объема и стоимости картофеля.
Решение:
а) Индивидуальный индекс физ. объема.
iq =
=
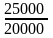 =
1,25 (или 125%)
=
1,25 (или 125%)
Мы получили, что физ. объем проданного картофеля в текущем периоде по сравнению с базисным возрос на 25% (125%-100%), или на 5000 кг, и составил 125% от уровня продаж базисного периода.
б) Индивидуальный индекс цен.
ip =
=
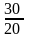 =
1,5 (или 150%)
=
1,5 (или 150%)
Мы получили, что уровень цен на картофель в текущем периоде по сравнению с базисным возрос на 50% (150%-100%), или на 10 руб. за кг., и составил 150% от уровня цен базисного периода.
в) Индивидуальный индекс товарооборота.
ipq =
=
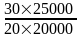 =
=
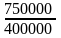 =
1,875 (или 187,5%)
=
1,875 (или 187,5%)
Мы получили, что товарооборот картофеля в текущем периоде по сравнению с базисным возрос на 87,5% (187,5%-100%), или на 350000 руб. (750000 – 400000), и составил 187,5% от товарооборота базисного периода. Рост товарооборота картофеля в текущем периоде по сравнению с базисным произошел как за счет роста цен, так и за счет роста физ. объема продаж.
Пример № 2
Определить индивидуальные индексы цены, физ. объема и стоимости мясных продуктов, если известно следующее:
товар |
Средняя цена за единицу (долл.) |
Сумма реализации (тыс. долл.) |
||
Базисный период |
Отчетный период |
Базисный период |
Отчетный период |
|
Мясные продукты |
2,2 |
2,0 |
10,0 |
12,4 |
Решение:
а) Индивидуальный индекс цены.
ip =
=
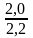 =0,909
(или 90,9%)
=0,909
(или 90,9%)
Мы получили, что уровень цен на мясные продукты в текущем периоде по сравнению с базисным уменьшился на 9,1% (90,1%-100%), или на 0,2 долл. за ед., и составил 90,9% от уровня цен базисного периода.
б) Индивидуальный индекс товарооборота.
ipq =
=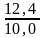 =
1,24 (или 124%)
=
1,24 (или 124%)
Мы получили, что товарооборот мясных продуктов в текущем периоде по сравнению с базисным возрос на 24% (124%-100%), или на 2400 долл.(12400 – 10000), и составил 124% от товарооборота базисного периода. Очевидно, что рост товарооборота мясных продуктов в текущем периоде по сравнению с базисным произошел из-за роста физ. объема продаж.
в) Индивидуальный индекс физ. объема
iq =
=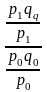 =
=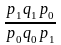 =
=
 =
= =
1,364 (или 136,4%)
=
1,364 (или 136,4%)
Мы получили, что физ. объем проданных мясных продуктов в текущем периоде по сравнению с базисным вырос на 36,4% (136,4% - 100%), или на 1654 кг (12400/2,0 – 10000/2,2) и составил 136,4% от уровня продаж базисного периода.
Билет №24
Построение индексов в агрегатной форме. Индексируемая величина и статистический вес.
Агрегатный индекс – сложный относительный показатель, который характеризует среднее изменение социально-экономического явления, состоящего из несоизмеримых элементов. Особенность этой формы индекса состоит в том, что в агрегатной форме непосредственно сравниваются две суммы одноименных показателей. Числитель и знаменатель агрегатного индекса представляют собой сумму произведений двух величин, одна из которых меняется (индексируемая величина), а другая остается неизменной в числителе и знаменателе (вес индекса). Агрегатные индексы – основная форма общих индексов.
Индексируемая величина – признак, изменение которого изучается (цена товаров, курс акций и т.д.)
Вес индекса – величина постоянная, одинаковая в числителе и знаменателе, служит для соизмерения индексируемых величин.
Методика построения агрегатного индекса предусматривает ответ на три вопроса:
А) какая величина будет индексируемой;
Б) по какому составу разнородных элементов явления необходимо исчислить индекс;
В) что будет служить весом при расчете индекса.
При этом, если строится индекс количественного показателя, то веса берутся за базисный период; при построении индекса качественного показателя используются веса отчетного периода.
1) Агрегатный индекс стоимости продукции
Стоимость продукции – это произведение количества продукции в натуральном выражении (q) на ее цену (p).
Индекс стоимости продукции, или
товарооборота (Ipq) представляет
собой отношение стоимости продукции
текущего периода (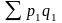 )
к стоимости продукции в базисном периоде
(
)
к стоимости продукции в базисном периоде
(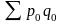 )
и определяется по формуле: Ipq =
)
и определяется по формуле: Ipq =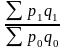 .
.
Такой индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным, или сколько процентов составляет рост (снижение) стоимости продукции. Если из значения индекса стоимости вычесть 100% (Ipq – 100%), то разность покажет, на сколько процентов возросла (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным. Разность числителя и знаменателя ( - ) показывает, на сколько рублей увеличилась (уменьшилась) стоимость продукции в текущем периоде по сравнению с базисным.
2) Агрегатный индекс физического объема продукции
Индекс физического объема продукции – это индекс количественного показателя. Здесь индексируемая величина – количество продукции в натуральном выражении, а вес – цена. Только умножив несоизмеримые между собой количества разнородной продукции на их цены, можно перейти к стоимостям продукции, которые будут уже величинами соизмеримыми. Так как индекс физического объема – индекс количественного показателя, то весами будут цены базисного периода. Тогда формула индекса примет следующий вид:
Iq = , где в числителе дроби – условная стоимость произведенных в текущем периоде товаров в ценах базисного периода, а в знаменателе – фактическая стоимость товаров, произведенных в базисном периоде.
Данный индекс показывает, во сколько
раз возросла (уменьшилась) стоимость
продукции из-за роста (снижения) объема
ее производства или сколько процентов
составляет рост (снижение) стоимости
продукции в результате изменения
физического объема ее производства.
Если из значения этого индекса вычесть
100% (Iq – 100%), то разность покажет,
на сколько процентов возросла (уменьшилась)
стоимость продукции в текущем периоде
по сравнению с базисным из-за роста
(снижения) объема ее производства.
Разность числителя и знаменателя (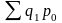 -
-
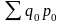 )
показывает, на сколько рублей изменилась
стоимость продукции в результате роста
(уменьшения) ее объема.
)
показывает, на сколько рублей изменилась
стоимость продукции в результате роста
(уменьшения) ее объема.
3) Агрегатный индекс цен
Индекс цен является наиболее широко распространенным показателем инфляции.
Индекс цен – индекс качественного показателя. Индексируемая величина – цена товара, вес – количество произведенных товаров. Умножив цену товара на его количество, получаем величину, которую можно суммировать и которая представляет собой показатель, соизмеримый с другими подобными ему величинами. Так как индекс цен – индекс качественного показателя, то весом будет количество произведенной продукции текущего периода. Тогда индекс цен определяется по следующей формуле: Ip= , где в числителе дроби – фактическая стоимость продукции текущего периода, а в знаменателе – условная стоимость тех же товаров в ценах базисного периода.
Индекс показывает, во сколько раз
возросла (уменьшилась) стоимость
продукции из-за изменения цен или сколько
процентов составляет рост (снижение)
стоимости продукции в результате
изменения цен. Если из значения данного
индекса вычесть 100% (Ip - 100%), то
разность покажет, на сколько процентов
возросла (уменьшилась) стоимость
продукции из-за изменения цен, а разность
числителя и знаменателя (
-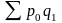 )
– на сколько рублей изменилась стоимость
продукции в результате роста (снижения)
цен.
)
– на сколько рублей изменилась стоимость
продукции в результате роста (снижения)
цен.
При этом: Ip Iq = Ipq
Пример № 1
Определить общие индексы цен, товарооборота и физического объема, если известно следующее:
Товары |
Средняя цена за единицу (долл.) |
Сумма реализации (тыс. долл.) |
||
Базисный период |
Отчетный период |
Базисный период |
Отчетный период |
|
Мясные продукты |
2,2 |
2,0 |
10,0 |
12,4 |
Молочные продукты |
0,5 |
0,6 |
8,0 |
9,2 |
Решение:
А) Мясные продукты:
 =
=
 =>
q1=
=>
q1=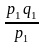 =
=
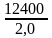 = 6200 ед.;
= 6200 ед.;
 =
=
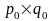 =>
q0=
=>
q0= =
=
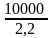 =4545
ед.
=4545
ед.
Б) Молочные продукты:
=
=>
q1=
=
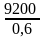 = 15333 ед.;
= 15333 ед.;
=
=>
q0=
=
 = 16000 ед.
= 16000 ед.
1) Индекс цен:
Ip=
=
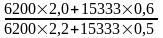 =
=
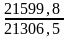 =1,014
(или 101,4%).
=1,014
(или 101,4%).
Мы получили, что общий уровень цен по данным продуктам возрос на 1,4% (101,4%-100%), или в 1,014 раз, и составил 101,4% от прежнего. Перерасход потребителя составил 293,3 (21599,8-21306,5).
2) Индекс физического объема:
Iq =
=
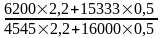 =
=
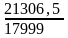 =
1,184 (или 118,4%).
=
1,184 (или 118,4%).
Мы получили, что общий уровень физ. объема возрос на 18,4% (118,4% - 100%), или в 1,184 раз, и составил 118,4% от прежнего уровня.
3) Индекс товарооборота:
Ipq =
=
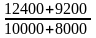 =
=
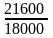 =
1,2 (или 120%).
=
1,2 (или 120%).
Мы получили, что общий уровень товарооборота возрос на 20% (120%-100%), или в 1,2 раз, и составил 120% от прежнего уровня. Рост этого показателя произошел в основном за счет роста объема потребления. Потребитель стал в общем потреблять продукции на 3600 долл. (21600 – 18000) больше.
Используя взаимосвязь индексов, проверим правильность вычислений:
Ip Iq = Ipq=1,014 1,184=1,2.
Пример № 2
Что произошло с физическим объемом импорта страны А, если общая стоимость всех закупок возросла в отчетном периоде по сравнению с базисным на 12%, а индекс цен по импорту составил 96%?
Дано:
Ipq = 112%
Ip= 96%
Найти Iq
Решение:
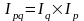 =>
=>
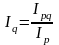 =
=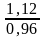 =1,167
(или 116,7%).
=1,167
(или 116,7%).
Ответ: Физический объем импорта страны А возрос на 16, 7% (116,7% - 100%), или в 1,167 раз, и составил 116,7% от прежнего уровня.
Билет №25
Средние индексы, тождественные агрегатным.
Кроме агрегатных, индексов в статистике применяются и средневзвешенные. Их рассчитывают, если имеющейся информации недостаточно, чтобы рассчитать общий агрегатный индекс. Например, если нет данных о ценах, но есть – о стоимости продукции в текущем периоде и об индивидуальных индексах цен по каждому товару, то общий индекс цен как агрегатный определить нельзя, но можно вычислить его как средний из индивидуальных. Если же не известны количества произведенных отдельных видов продукции, но известны индивидуальные индексы и стоимость продукции базисного периода, то можно определить общий индекс физического объема как средневзвешенную величину.
Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов. Средний индекс производный, он получается в результате преобразования агрегатного, а следовательно тождествен ему.
При исчислении средних индексов используются две формы средних: арифметическая и гармоническая.
Средний арифметический индекс тождествен агрегатному, если весами индивидуальных индексов будут слагаемые знаменателя агрегатного индекса.
Средний
арифметический индекс физического
объема вычисляется по формуле:
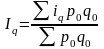 .
Весами в формуле является стоимость
продукции базисного периода. Так как
.
Весами в формуле является стоимость
продукции базисного периода. Так как
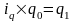 ,
то формула этого индекса легко
преобразуется в формулу:
,
то формула этого индекса легко
преобразуется в формулу:
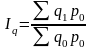 .
.
Средние арифметические индексы чаще всего применяются на практике для расчета сводных индексов количественных показателей. Индексы качественных показателей обычно определяются по формуле средней гармонической взвешенной величины.
Средний
гармонический индекс тождествен
агрегатному, если индивидуальные индексы
взвешены с помощью слагаемых числителя
агрегатного индекса. Например, индекс
цен можно вычислить по формуле:
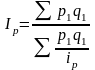 ,
где весами является стоимость продукции
текущего периода. Так как
,
где весами является стоимость продукции
текущего периода. Так как
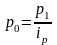 ,
то формула может быть легко преобразована
в формулу
,
то формула может быть легко преобразована
в формулу
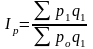 .
.
Средние индексы также широко применяются для анализа рынка ценных бумаг. Наиболее известным является индекс Доу-Джонса, который определяется как средний арифметический индекс значений курсов акций, котирующихся на Нью-йоркской фондовой бирже.
Пример №1
По нижеследующим данным определить индекс физического объема продукции:
Виды изделий |
Выпуск продукции в мае (в млн. руб.) |
Изменение физического объема продукции в июне по сравнению с маем (%) |
Туфли женские |
30 |
+15 |
Туфли мужские |
25 |
+10 |
Туфли детские |
10 |
-20 |
Решение:
1) Индивидуальные индексы объема:
Туфли
женские:
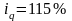 ;
;
Туфли
мужские: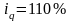 ;
;
Туфли
детские: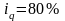 .
.
2) Средний арифметический индекс физического объема:
=
 =
=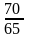 =1,077
(107,7%).
=1,077
(107,7%).
В среднем физический объем продукции в июне увеличился по сравнению с маем на 7,7% и составил 107,7% от уровня мая.
Пример №2
Определить средний размер изменения цен на товары А и Б в 2006 году по сравнению с 2005 годом по следующим данным:
Товары |
Реализовано в 2006г. (млн. руб.) |
Изменение цен в 2006г. по сравнению с 2005г. (%) |
А |
12 |
-3 |
Б |
20 |
+2 |
Решение:
1) Индивидуальные индексы цен:
А:
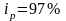 ;
;
Б:
 .
.
2)Средний гармонический индекс цен:
= =
= =0,999
(99,9%).
=0,999
(99,9%).
В среднем цены на продукцию в 2006г. уменьшились по сравнению с 2005г. на 0,1% и составили 99,9% от уровня 2005г.
Билет №26
Выбор базы и весов при построении индексов. Системы индексов (цепных и базисных).
Системой индексов называется ряд последовательно построенных индексов. Такие системы характеризуют изменения, происходящие в изучаемом явлении в течение исследуемого периода времени.
В зависимости от базы сравнения системы индексов бывают базисными и цепными.
Система базисных индексов – это ряд последовательно вычисленных индексов одного и того же явления с постоянной базой сравнения, т.е. в знаменателе всех индексов находится индексируемая величина базисного периода.
Система цепных индексов – это ряд индексов одного и того же явления, вычисленных с меняющейся от индекса к индексу базой сравнения.
В экономико-статистических исследованиях выбор системы индексов (базисные или цепные) проводится в зависимости от цели анализа. Базисные индексы дают более наглядную характеристику общей тенденции развития исследуемого явления, а цепные – четче отражают последовательность изменения уровней во времени.
Системы цепных и базисных индексов могут быть построены для индивидуальных и общих индексов.
Между цепными и базисными индексами существуют различные виды связи.
Если известны цепные индексы, то путем их последовательного перемножения можно получить базисные индексы.
Например,
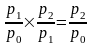 или
или
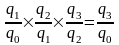 .
.
Зная последовательные значения базисных индексов, легко рассчитать на их основе цепные индексы.
Например,
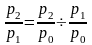 или
или
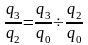 .
.
Системы базисных и цепных индексов могут быть построены для агрегатных индексов.
Например, цепные индексы стоимости:
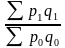 ;
;
 ;…;
;…;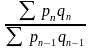 или базисные индексы стоимости:
или базисные индексы стоимости:
;
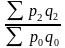 ;…;
;…;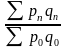 .
.
Формирование системы индексов цен и физического объема отличаются от рассмотренных выше, т.к. при построении систем этих индексов можно использовать постоянные или переменные веса.
Система
индексов с постоянными весами –
система сводных индексов одного и того
же явления, вычисленных с весами, не
меняющимися при переходе от одного
индекса к другому. Постоянные веса
позволяют исключить влияние изменения
структуры на величину индекса. Например,
система базисных индексов физического
объема продукции с постоянными весами
(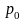 ):
):
;
;…;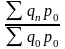 - и система цепных индексов физического
объема с постоянными весами:
;
- и система цепных индексов физического
объема с постоянными весами:
;
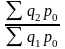 ;…;
;…; .
.
При этом между цепными и базисными индексами с постоянными весами также существует связь.
Например, перемножая цепные индексы получаем соответствующий базисный: = , а при деление базисных индексов получаем соответствующий цепной: = .
Система индексов с переменными весами – система сводных индексов одного и того же явления, вычисленных с весами, последовательно меняющимися от одного индекса к другому. Переменные веса – веса отчетного периода.
Например,
система базисных индексов цен с
переменными весами:
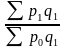 ;
;
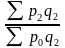 ;…;
;…;
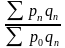 - и система цепных индексов цен с
переменными весами:
;
- и система цепных индексов цен с
переменными весами:
;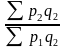 ;…;
;…;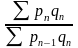 .
.
Для общих индексов рассчитанных с переменными весами взаимосвязь между цепными и базисными индексами отсутствует.
Пример:
Имеются следующие данные о производстве топлива нефтегазовым комплексом РФ:
Топливо |
1999 |
2000 |
2001 |
Нефть (млн. т) |
295 |
313 |
337 |
Газ (млрд. м3) |
592 |
584 |
581 |
Проведите анализ представленных в таблице данных, рассчитав цепные и базисные сводные индексы физического объема продукции, если известно, что в 1999г. средняя оптовая цена за нефть 1000 руб. за 1т., за газ – 58 руб. за 1000 м3.
Решение:
Базисные:
2000г.:
=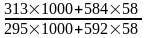 =
=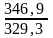 =1,053
(105,3%);
=1,053
(105,3%);
2001г.:
=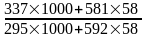 =
=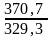 =1,126
(112,6%).
=1,126
(112,6%).
Цепные:
2000г.: = = =1,053 (105,3%);
2001г.:
=
=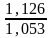 =1,069
(106,9%).
=1,069
(106,9%).
Изменение уровня физического объема продукции (стоимости за счет физического объема) в 2000г. по сравнению с 1999г. составило 5,3%. В 2001г. физический объем продукции (стоимость за счет физического объема) увеличился по сравнению с 1999г. на 12,6% , а по сравнению с 2000г. на 6,9%. Это происходило в основном за счет прироста физического объема продаваемой нефти, в то время как поставки газа сокращались.
Пример:
Физический объем потребительских товаров и услуг в регионе в феврале по сравнению с предшествующим месяцем возрос на 3,4%. Как изменился физический объем в марте по сравнению с февралем, если общий рост цен с января по март составил 110,7%?
Решение:
=103,4%
=
= =1,07
(107%).
=1,07
(107%).
Физический объем потребительских товаров и услуг с февраля по март увеличился на 7% и в марте составил 107% от уровня февраля.
Билет №27
Предмет и метод статистики населения, ее задачи.
Население – объект всестороннего исследования, поскольку оно является непосредственным участником производственного процесса и потребителем его результатов. Население как предмет изучения в статистике представляет собой совокупность людей, проживающих на определенной территории и непрерывно возобновляющихся за счет рождений и смертей. В статистике население единицей наблюдения чаще всего является отдельный человек как индивидуум, однако может быть и семья. Также может быть и домохозяйство. В отличие от семьи под домохозяйством понимают совместно проживающих и ведущих общее хозяйство людей. Объектом статистического наблюдения в статистике населения могут быть разные совокупности: население в целом (постоянное или наличное), отдельные группы населения (трудоспособное население, безработные, пенсионеры, городское население или сельское, мужчины или женщины и т.д.), молодые семьи, родившиеся за год или умершие и т.д. Объект и единица наблюдения выбираются в зависимости от цели исследования.
Источниками статистики населения являются текущий учет и единовременные наблюдения в виде сплошных или выборочных переписей. Первоисточником сведений о населении являются переписи.
Основные задачи статистики населения:
Определение численности населения и его распределения по территории страны;
Изучение состава населения (по полу, возрасту, национальной принадлежности, социальному положению, образованию и т.д.);
Изучение естественного движения населения (рождаемость, смертность, естественный прирост населения, заключение и расторжение браков);
Изучение миграции населения;
Социальная характеристика населения.
№28 Основные источники статистической информации о населении страны
Выделяют 3 основных источника информации о населении:
Перепись населения – первоисточник сведений о населении, дает наиболее полные и точные сведения о численности населения и его составе.
Текущий учёт:
а) учёт естественного движения населения (на основе материалов органов ЗАГС – отделов записей актов гражданского состояния1)
б) учёт механического движения населения (по данным Федеральной миграционной службы (ФМС России, Росстат), её территориальные органов, органов МВД (иммиграция), паспортных столов (факт прибытия), по месту жительства и др.).
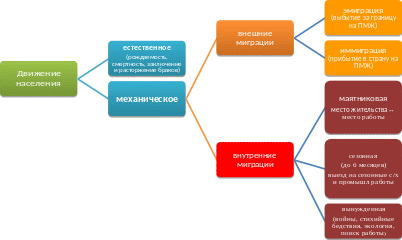
Выборочные обследования (микропереписи) – проводятся за несколько лет до всеобщей переписи.
№ 29. Переписи населения: определение, научные критерии организации
Перепись населения – специальное, научно организованное статистическое мероприятие, направленное на сбор наиболее полной информации о численности, составе и размещении населения страны.
Научные критерии организации переписи населения:
Всеобщность: перепись проводится на всей территории и для всего населения страны без дискриминации.
Периодичность: в России –раз в 10 лет (в периоды наибольшей оседлости населения: осень или зима); в Западной Европе – раз в 5 лет.
Одномоментность: одинаковые сроки на всей территории страны.
Единая программа
Поимённость переписи: информация собирается по каждому человеку в отдельности для дальнейшего обобщения
Самоопределение: сведения собираются со слов опрашиваемых (экспедиционный опрос: листы заполняют представители органов со слов опрашиваемых)
Своевременность обработки, анализа и публикации данных.
№30.Всероссийские переписи населения 2002 и 2010 гг.: задачи, особенности организации, программы переписи, значение собранной статистической информации, основные итоги.
Перепись населения - один из важнейших источников информации о населении. В наиболее общем виде перепись населения - научно организованный процесс сбора, обработки и анализа данных о численности и составе населения.
Перепись проводится для получения информации об изменениях, происходивших в населении в межпереписной период, и последующей корректировки на этой основе оценок численности и состава населения по территориям, подготовки базы для перспективных расчетов.
Все сведения о населении собираются по состоянию на определенный (критический) момент. Это конкретный день и час, к которому приурочивают собираемые сведения для обеспечения сопоставимости полученных данных. Умершие до этого момента и родившиеся после этого момента в ходе переписи не учитываются и в численность населения не включаются. Для проведения переписи, как правило, выбирают время, когда население наименее подвижно - за пределами сезона отпусков, каникул, праздничных дней.
Научные критерии проведения переписи см № 29.
На территории России всеобщая перепись проводилась 9 раз:
В Российской империи (1897)
В СССР (1926, 1939, 1959, 1970, 1979, 1989)
В Российской Федерации ( 2002, 2010)
Перепись 2010 года проводилась в период 14 – 25 октября.
Цель переписной кампании — сбор сведений о лицах, находящихся на определённую дату на территории Российской Федерации. Обработка полученных сведений, формирование итогов, их публикация и распространение будут осуществлены в 2010—2013 годах.
Своеобразие всероссийских переписей населения (2002 и 2010):
Открытие переписных пунктов
Информация могла даваться не только приходящему на дом переписчику, но и по телефону
1 член семьи мог предоставлять информацию о всех членах своей семьи.
В отличие от советских переписей указывались не только отдельные граждане, но и домашние хозяйства (семья – родственные отношения, дом.хоз. – общий бюджет, место проживания( вкл садовников, нянь))
Участие в переписях сугубо добровольно.
Программы переписей практически полностью совпадают, что обеспечивает возможность сопоставления результатов переписей.
Перепись 2010 проводилась с использованием 3 типов бланков:
П1, П2 – для жилищной переписи
Л1, Л2 – листы основной переписи
В1, В2 – листы временной переписи
П1 и П2 (вопросы о типе жилища, времени постройки дома, материал наружных стен дома, благоустройство и условия проживания; тип жилого помещения (отдельная/коммунальная квартира), площадь квартиры, число комнат, телекоммуникации).
Л1 и Л2:
Пол
Дата рождения
Место рождения
Состояние в браке (графы: брак зарегистрирован или нет, разведен официально, разошёлся, никогда не состоял в браке, вдовец)
Гражданство: учёт граждан РФ, лиц с двойным гражданством. Граждан иностранных государств и лиц без гражданства)
Национальная принадлежность (необязательно).
Образование (с 10 лет, для тех, кто не имеет – вопрос об умении читать и писать)
Учёная степень (кандидат или доктор наук)
Посещение ребёнком дошкольного учреждения (дети, не посещающие школу до 10 лет)
Владение языками (владение русским, владение другими тремя языками (в 2002 можно было указывать неограниченное кол-во), владение языком жестов, родной язык)
Источники средств к существованию (трудовая деятельность, личное подсобное хозяйство, стипендия, пенсия, пенсия по инвалидности, пособие, пособие по безработице; сбережения, дивиденды, проценты; сдача имущества в наём или аренду, доход от патентов и авторских прав; иждивение, алименты; иной источник)+ указать основной источник
Занятость и безработица
Миграция ( с какого периода проживаете в данном населенном пункте, проживание в октябре 2009 года, в сельском или городском насел пункте;
(для женщин старше 15): сколько детей родили, дата рождения первого ребёнка.
В1 и В2 (для временно проживающих на территории РФ, сокращённый опрос):
Пол
Год рождения
Страна постоянного проживания
Цель приезда
Для приехавших с целью работы, учёбы:
Продолжительность проживания в РФ
Страна рождения
Гражданство.
