31. Структурные схемы дискретных фильтров.

Широко используются 2 формы изображения структурной схемы фильтра: прямая форма и каноническая форма.

Прямая форма соответствует исходному разностному уравнению.

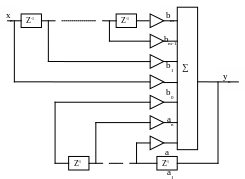
Схема содержит M+N элементов памяти, M+N+1 умножителей и сумматор с N+M+1 входами. Период следования отсчетов равен интервалу дискретизации ∆t.

Каноническая форма

Эта форма реализации дискретного фильтра основана на преобразовании выражения для передаточной функции.

;

;

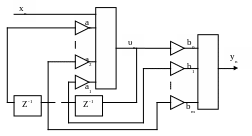
Эта схема позволяет сэкономить на объеме памяти.

32. Линейные модели и расчет спектральной плотности мощности.

АРСС модели.

Многие последовательности отсчетов сигнала x_n, n=0,1….N, представляющего собой сумму детерминированных и случайных сигналов м.б. достаточно хорошо аппроксимированы выходным сигналом линейного фильтра.

, где - входной сигнал фильтра

Эта модель в виде линейного фильтра называется АРСС моделью (авторегрессии со скользящим средним). В задачах входной сигнал считают белым шумом с дисперсией δ_n. Используя это можно смоделировать сигнал и подсчитать спектр.

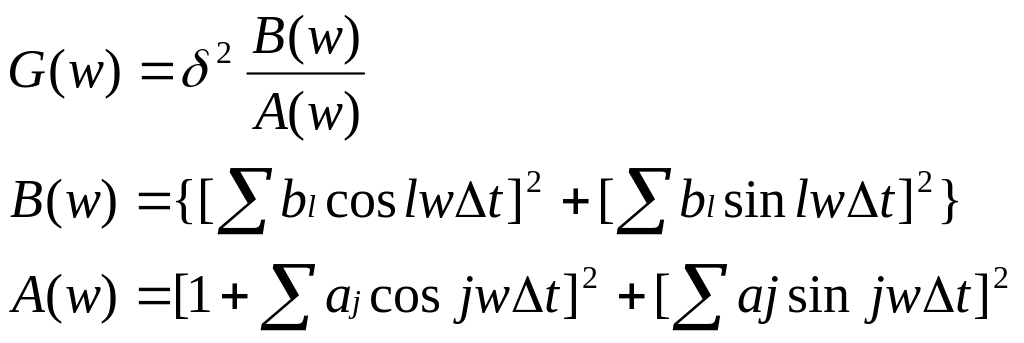
Если все a_j=0, то получаем модель скользящего среднего(СС):

, A(w)=1

Если b₀=1, b_l=0, то получим модель АР:

, B(w)=1

У модели скользящего среднего в уравнении присутствуют 0, поэтому ее называют нулевой моделью; у АР модели нули отсутствуют, но есть полюса, ее называют чисто полюсной моделью.

Принципиально все 3 модели применимы в одинаковой степени, т.к. существует метод, который позволяет любую из этих моделей представить любой из 2х оставшихся. Для каждой из этих моделей процесс вычисления параметров разный.

33.Устойчивость дискретных фильтров.

Фильтр называется устойчивым, если при любом ограниченном по амплитуде входном сигнале {x_n} выходной сигнал фильтра является ограниченным.

│{x_n}│≤B → │{y_n}│≤D

│y_n│≤D (при любом n), n→∞, D=const и не зависит от n

Исходя из этого определения, нерекурсивный фильтр всегда устойчив.

Рекурсивный фильтр – это фильтр с ОС, поэтому он м.б. неустойчивым. В общем случае, рекурсивный фильтр устойчив, если устойчивым является решение соответствующего однородного линейного разностного уравнения.

- однородное разностное уравнение

Общий вид решения этого уравнения:

- это решение должно быть устойчивым

Здесь Z_1, Z₂,…Z_n – корни характеристического уравнения, которое получается из разносного:

1+a₁Z^-1+a₂Z^-2+….+a_nZ^-N=0

Коэффициенты c_l – это постоянные коэффициенты, которые определяются начальными условиями.

│Z_l│<1, т.е. все корни по модулю должны быть меньше 1. На комплексной плоскости корни должны лежать внутри единичной окружности.

Корни характеристического уравнения – полюса передаточной функции. Рекурсивный фильтр устойчив тогда, когда его полюса лежат внутри единичной окружности. Однако, устойчивость м.б. обеспечена и при нахождении полюсов за единичной окружностью. Это возможно, когда знаменатель передаточной функции имеет корни в этих же точках. Из выражения

следует еще одно условие устойчивости:

Эти критерии устойчивости относятся только к линейным дискретным фильтрам, т.е. когда отсутствует квантование отсчетов, и все арифметические операции выполняются точно.