18) Собственные значения и собственные волновые функции операторов м и м.
орбит.квант.число
l=k+m
-мех.момент
квантовой часитцы дискрет.
-полином
Лагранжа
,
-опер.мв2
и мз комутируют между
собой
19) Атом водорода.
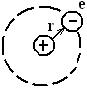1)
Помест.ядро в начало коорд. 2) Будем
считать, что маса ядра значит. больше
массы элект; ядро неподвиж.. Это позволяет
раздел.ядерную и электрон. подсистемы
и рассматр.только
движ.электрона.
3) Будем считать заряд электр.тонечным,
который подчиняется закону Кулона:
;
Исполь.стац.
Ур. Шредингера
Запишем это ур. в
системе единиц Хартри: ед. массы- масса
электрона, ед. заряда – заряд электрона,
ед. действия – постоянная Планка.
.
Распишем это
уравнение
;
Зная то решение
правой части имеет вид:
;
20) Энергетический спектр и волновые функции атома водорода.
,
где
орбитальное квантовое число. Момент
имеет проекции:
,
;
запишем
,
(:
)
.
Коэффициенты обращаются в бесконечность
при
эти точки надо подавить при нахождении
волн. ф-ии
.
Потенциальная энергия взаимодействия
эл-на с ядром уменьшается с удалением
от ядра и стремится к некоторой постоянной
,
при
.
Решение сильно зависит о того что
:
(*);
точное решение будем искать в
,
-для
подавления особых точек уравнения. Из
анализа поведения ф-ии вытекает, что
.
Найдем 1 и 2 производную и подставим в
ур.. (*) и пол ур.
.
Получим ур. Относительно членов ряда
.
Это ур. может выполняться, только если
все коеф-ты при
равно
нулю. Найдем коеф. При
:
ряд не сходится, чтобы сошлось, надо
оборвать ряд.
,
значит
,
где
- главное квантовое число,
,
,
где
-
полином Лабера
,
Состояние задаваемое с квантовими
числами наз. атомной
орбиталью
21) Квантовые числа в атоме водорода и их смысл.
,
- главное квантовое число, и указывает
на величину энергии
,
,
орбитальное
квантовое число и ук. на вел. момента
импульса
,
,
– магнитное кв. число, и ук. на вел.
проекции момента импульса
,
на некоторое произвольное направление
.Три
величины
вполне
определяют волновую функцию
и поэтому образуют полный набор величин;
число их отвечает количеству степеней
свободы….
22) Магнетон атома водорода.
Т.к.электр.облако может вращаться вокруг ядра,а эл.обладает зарядом,то должны возникать круговые токи , которые должны рождать магнитный момент
,
,
-движ.заряда
по радиус.отсуцт.
-движ.зар.поуглу
оцуцтвуует.Вэл.поле сущ.движ.только по
углу
S-площадь
которую охват.круговой ток(труюочка)
,
,
-магнетон
бора
23) Геометрическая интерпретация волновых функций.
24) Теория представлений.
,
,
,
,
,
-
поворот проекций
,
,
Собственные
волновые функции ведут себя как орты,
образуя трехмерное ортонормальное,
ортогональное пространство, тогда
представляют собой проекции
,
,
,
представляет собой
функцию
в
представлении.
,
,
где
представляют собой волновые функции в
представлении.
