24. Решение систем линейных уравнений со ступенчатой матрицей
Ступенчатая матрица — матрица, имеющая m строк, у которой первые r диагональных элементов ненулевые, r ≤ m, а элементы, лежащие ниже диагонали и элементы последних m − r строк равны нулю:
25. Общее решение систем линейных уравнений. Главные и свободные неизвестные.
Определение
5.1. Системой m линейных
уравнений с n неизвестными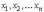 
называется
система S вида
,
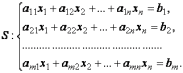где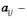 
коэффициенты
при неизвестных,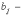 
свободные
члены (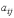
, 
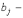заданные
числа).
Определение
5.2. Решением
системы 
называется
упорядоченный набор действительных
чисел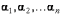 
,
при подстановке которых в каждое
уравнение системы вместо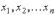 
соответственно
будут получены верные числовые равенства.
Определение
5.3. Система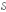 
называется
совместной (несовместной), если она
имеет хотя бы одно решение (не имеет
решений).
Определение 5.4. Совместная система линейных алгебраических уравнений называется определённой (неопределённой), если она имеет единственное решение (множество решений).
Определение
5.5.
Матрица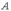 
,
составленная из коэффициентов при
неизвестных, называется основной
матрицей системы
:
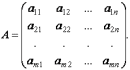
Матрица
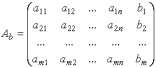
называется расширенной матрицей этой системы.
Замечание. Система может быть переписана в так называемом матричном виде:
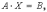
где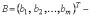 
вектор-столбец
свободных членов системы.
Определение 5.6. Если все свободные члены системы уравнений равны нулю, то такая система называется однородной, если же хотя бы один свободный член отличен от нуля, система называется неоднородной.
Теорема 5.1. Однородная система линейных уравнений имеет ненулевое решение тогда и только тогда, когда определитель основной матрицы системы равен нулю.
Определение 5.7. Элементарными преобразованиями системы линейных уравнений называют следующие операции:
1) сложение обеих частей одного уравнения с соответствующими частями другого, умноженных на одно и то же число, не равное нулю;
2) перестановка уравнений местами;
3) удаление из системы уравнений, являющихся тождествами.
Рассмотрим основные методы решения систем линейных уравнений.
26. Геометрическая интерпретация систем линейных уравнений в случае двух или трех неизвестных
Если каждое решение линейного уравнения относительно двух неизвестных ax+by+c = 0, в котором коэффициенты при неизвестных не равны нулю одновременно, изображать точкой плоскости с координатами (x,y), то множествовсех таких точек образует некоторую прямую .Поэтому множеству решений системы из двух таких уравнений соответствует множество точек пересечения двух прямых. Система несовместна, если прямые параллельны; имеет единственное решение, если прямые пересекаются; имеет бесконечное множество решений, если прямые совпадают.
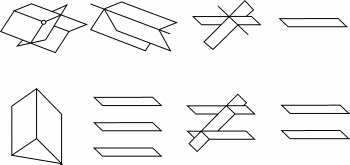
Множество точек пространства, соответствующих решениям линейного уравнения относительно трех неизвестных ax+by+cz+d = 0, в котором коэффициенты при неизвестных не равны нулю одновременно, является некоторой плоскостью Система из трех таких уравнений определяет множество точек пересечения этих плоскостей. Возможные при этом случаи изображены на предыдущем рисунке.Во всех случаях рассматриваются три плоскости, только в случаях (4я фигура) и (7я фигура) две из трех плоскостей совпадают, в случае (8я фигура)совпадают все три плоскости.