Вопрос 37 Преобразование матрицы билинейной формы при замене базиса
Матрица, представляющая билинейную форму в новом базисе, связана с матрицей, представляющей её в старом базисе, через матрицу, обратную матрице перехода к новому базису (матрице Якоби), через которую преобразуются координаты векторов.
Иными
словами, если координаты вектора в
старом базисе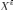 
выражаются
через координаты в новом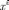 
через
матрицу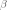 
,
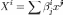или в матричной записи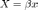 
,
то билинейная форма 
на
любых векторах 
и 
запишется,
как
,
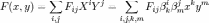то есть компоненты матрицы, представляющей билинейную форму в новом базисе, будут:
,
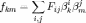или, в матричной записи:
,
,
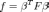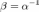где 
—
матрица прямого преобразования
координат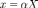 
.
Вопрос 38 Единственность симметричной билинейной формы, порождающей квадратичную форму
Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.
Определение
Пусть 
есть векторное
пространство над
полем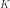 
и 
—
базис в
.
Функция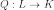 
называется
квадратичной формой, если её можно
представить в виде
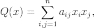
где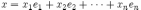 
,
а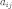 
—
некоторые элементы поля
.
Квадратичные
формы.
Определение.
Квадратичной формой или квадратичной
функцией на линейном пространстве L называется
функция к, значение которой на любом
векторе х определяется равенством k(х)
= b(x,x), где b — симметричная билинейная
функция.
По
заданной квадратичной форме к однозначно
определяется соответствующая симметричная
билинейная функция b. Действительно,
пусть х и у — произвольные векторы.
Тогда
k(х
+ у) = b(х + у, х + у) = b(х, х) + b(х, у) + b(у, х) +
b(у, у).
Отсюда,
используя b(y,x) = b(x,y), получаем, что
значение b на любых векторах выражается
через значения k.
Матрицей
квадратичной формы называется матрица
соответствующей билинейной функции.
Из
ранее выведенного мы имеем следующее
выражение значения квадратичной формы
через координатный столбец вектора:
k(x) =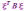 
.
Замена
базиса в данном случае очевидным образом
следует из замены базиса в билинейной
форме.
Вопрос39 Критерий Сильвестра положительной определенности квадратичной формы.
Критерий Сильвестра
Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.
Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.
Пусть квадратичная форма имеет в каком-то базисе матрицу
Тогда эта форма положительно определена, тогда и только тогда когда все её главные (угловые) миноры
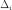положительны.
Форма отрицательно определена, если и
только если знаки
чередуются,
причём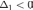 
.
Здесь главными минорами
матрицы 
называются
определители вида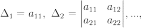
Для неотрицательно определённых матриц критерий действует только в одну сторону: если форма неотрицательно определена, то главные миноры неотрицательны. Обратное неверно. Например, матрица
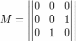
не является неотрицательно определённой — так как, например,
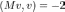для 
.
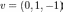В то же время все её главные миноры
равны 0, то есть неотрицательны.