Вопрос 34 Формула линейного функционала.

Линейный функционал — функционал, обладающий свойством линейности по своему аргументу:

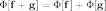
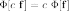
где   — линейный функционал,   и   — функции из его области определения,   — число (константа).

Иными словами, это линейное отображение из (некоторого) пространства функций во множество чисел — чаще всего подразумеваемых вещественными, или, еще иначе, линейный оператор, действующий из (некоторого) пространства функций в   (иногда в  ).

Выделяют следующие специальные виды функционалов:

• интегральный:

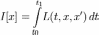
• терминальный:

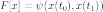
• смешанный (функционал Больца):

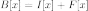
Вопрос 35

Пусть e₁, ..., e_n — базис в L. И пусть для векторов x и y из L заданы разложения

x = x₁·e₁+x₂·e₂+ ...+ x_n· e_n и y = y₁·e₁+ y₂·e₂+ ...+ y_n· e_n .

Тогда для билинейной формы φ(x , y) справедливо представление

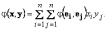
Обозначим φ_{i j} = φ(e_i , e_j). Тогда для билинейной формы формы φ(x , y) справедливо матричное представление φ(x , y) = x ^T·Φ·y:

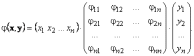
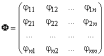
Матрица Φ называется матрицей билинейной формы.

Ранг матрицы билинейной формы не зависит от выбора базиса и называется рангом билинейной формы.

Дефектом билинейной формы называется разность между размерностью пространства и рангом билинейной формы: d = n − r.

Билинейная форма называется невырожденной, если её дефект равен нулю.

Вопрос 36 Матрица билинейной формы.

Пусть X — линейное пространство.

Функция b(x,y) , осуществляющая отображение X × X → R , называется билинейной формой, если она линейна по каждому аргументу, т.е. " x, y, z О X и " α, β О R

b(α x + β y, z) = α b(x, z) + β b(y, z);

b(x, α y + β z) = α b(x, y) + β b(x, z).

Билинейная форма называется симметричной, если " x, y О X    b(x, y) = b(y, x) .

Пусть e1, e2,  … , en — базис в Xn . Тогда " x,y О Xn

x  =    n xi ei ∑ i = 1  ,         y   =    n yj ej ∑ j = 1   .

Обозначим bij = b(ei, ej) . Воспользовавшись линейностью b(x, y) по обоим аргументам, получим:

b(x, y) = b  ж з и n xi ei ∑ i = 1   ,  n yj ej ∑ j = 1 ц ч ш    =    n xi yj b(ei, ej) ∑ i,j = 1    =    n bij xi yj ∑ i, j = 1   .

Квадратная матрица n –го порядка B = (bij)  называется  матрицей билинейной формы.

Обозначив X и Y координатные столбцы векторов x и y , билинейную форму можно записать в виде:

b(x,y) = XT · B · Y .

Преобразование матрицы билинейной формы при переходе к новому базису.

Пусть в Xn базисы e1, e2,  … , en и f1, f2,  … , fn связаны матрицей перехода C = (cik) по формуле

fi   =    n cikek ∑ k = 1   .

Обозначим Be и Bf матрицы билинейной формы b(x,y) в базисах e1, e2,  … , en и f1, f2,  … , fn соответственно. Тогда

Bf = CT · Be · C.

Справедливы следующие утверждения.

Матрица симметричной билинейной формы симметрична в любом базисе.

Если матрица билинейной формы симметрична в некотором базисе, то билинейная форма симметрична.