Вариант №11
1. Вычислить определитель матрицы:
2. Решить систему:
3. Найти ранг системы векторов, базисы и линейную зависимость между векторами:
4. Решить матричное уравнение 3B+XA = 2C, где
5. Даны четыре вектора:
Показать, что в векторы образуют базис в трехмерном пространстве и найти координаты вектора в этом базисе.
Вариант №12
1. Вычислить определитель матрицы:
2. Решить систему:
3. Найти ранг системы векторов, базисы и линейную зависимость между векторами:
4. Решить матричное уравнение XA-2B = 3C, где
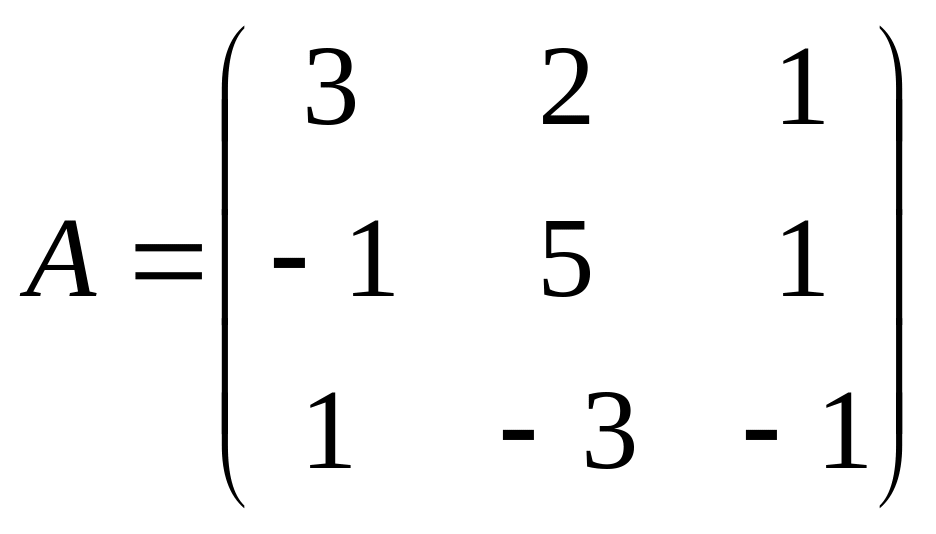
5. Даны четыре вектора:
Показать, что в векторы образуют базис в трехмерном пространстве и найти координаты вектора в этом базисе.
Вариант №13
1. Вычислить определитель матрицы:
2. Решить систему:
3. Найти ранг системы векторов, базисы и линейную зависимость между векторами:
4. Решить матричное уравнение XA = B, где
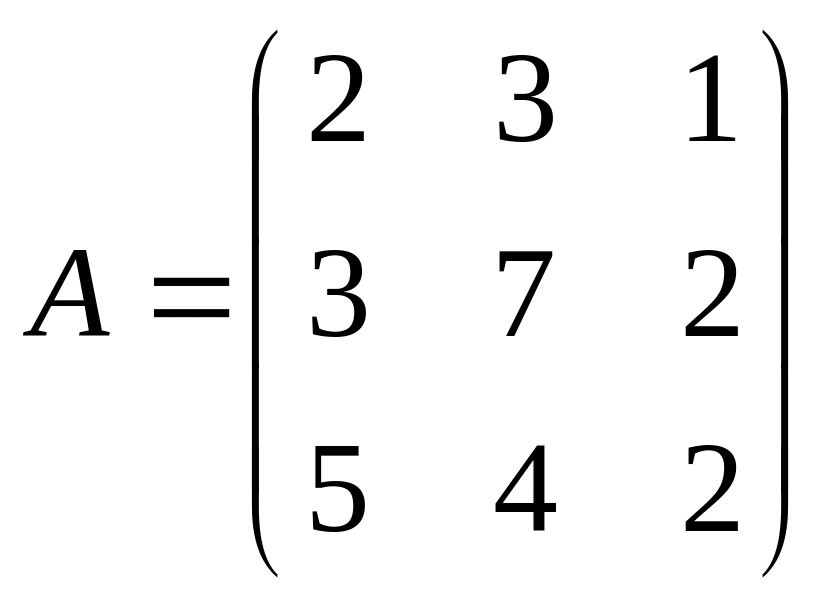
5. Даны четыре вектора:
Показать, что в векторы образуют базис в трехмерном пространстве и найти координаты вектора в этом базисе.
Вариант №14
1. Вычислить определитель матрицы:
2. Решить систему:
3. Найти ранг системы векторов, базисы и линейную зависимость между векторами:
4. Решить матричное уравнение AX = B, где
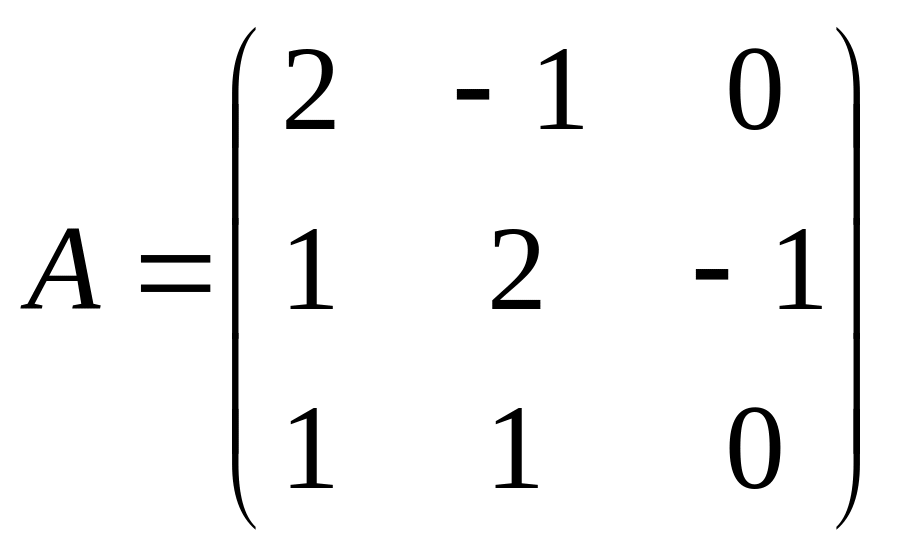
5. Даны четыре вектора:
Показать, что в векторы образуют базис в трехмерном пространстве и найти координаты вектора в этом базисе.
Вариант №15
1. Вычислить определитель матрицы:
2. Решить систему:
3. Найти ранг системы векторов, базисы и линейную зависимость между векторами:
4. Решить матричное уравнение XB = C, где
5. Даны четыре вектора:
Показать, что в векторы образуют базис в трехмерном пространстве и найти координаты вектора в этом базисе.
Вариант №16
1. Вычислить определитель матрицы:
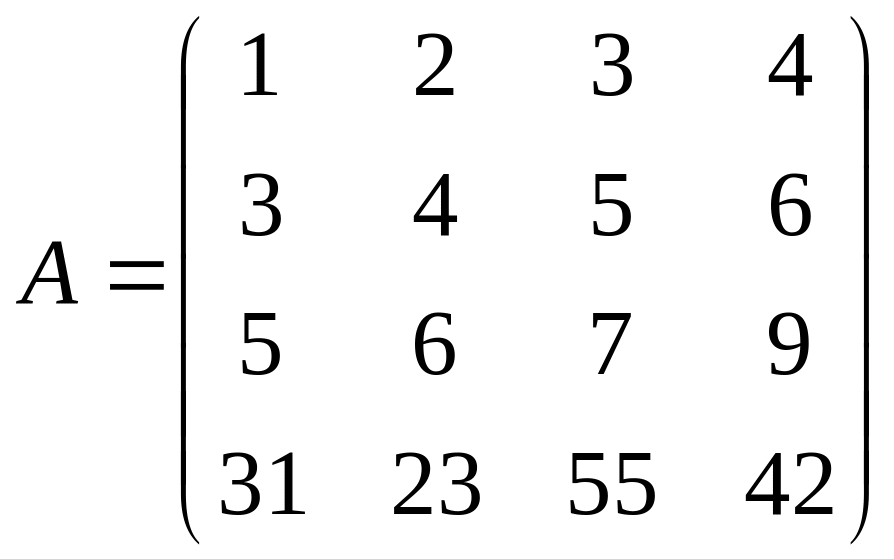
2. Решить систему:
3. Найти ранг системы векторов, базисы и линейную зависимость между векторами:
4. Решить матричное уравнение XA + 2C = 4B, где
5. Даны четыре вектора:
Показать, что в векторы образуют базис в трехмерном пространстве и найти координаты вектора в этом базисе.
Вариант №17
1. Вычислить определитель матрицы:
2. Решить систему:
3. Найти ранг системы векторов, базисы и линейную зависимость между векторами:
4. Решить матричное уравнение AXB = C, где
5. Даны четыре вектора:
Показать, что в векторы образуют базис в трехмерном пространстве и найти координаты вектора в этом базисе.