20.Угол между плоскостями. Условие параллельности и перпендикулярности плоскостей
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:
П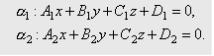
од углом между
двумя плоскостями будем понимать один
из двугранных углов, образованных этими
плоскостями. Очевидно, что угол между
нормальными векторами n1
и n2
плоскостей α1 и
α2 равен
одному из указанных смежных двугранных
углов
П
оэтому
Т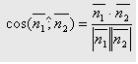
.к.
И
т
о
Условие параллельности двух плоскостей.
Две плоскости α1 и α2 параллельны тогда и только тогда, когда их нормальные векторы n1 и n2 параллельны, а значит
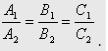
Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:
Условие перпендикулярности плоскостей.
Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, n1*n2 = 0 или A1A2 + B1B2 + C1C2 = 0
Таким образом,
P.S.
Примеры
тут:
http://www.toehelp.ru/theory/math/lecture19/lecture19.html
21.Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой
Чтобы составить уравнение плоскости, зная координаты точки плоскости
и
вектора нормали плоскости
можно использовать следующую формулу.
22.Нормированное уравнение плоскости.
Г
де:
-углы, образуемые нормальным вектором плоскости с осями координат; p- расстояние от начала координат до плоскости.
Приведение общего уравнения плоскости к нормальному виду:
Здесь
нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если произвольно, если D = 0 .
23.Прямая в пространстве. Общее уравнение прямой
Прямая в пространстве может быть задана также как пересечение двух плоскостей, если плоскости не параллельны:
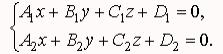
Все формы задания прямой в пространстве взаимосвязаны.
24.Параметрическое и Каноническое уравнение прямой.
Параметрическое:
Векторное уравнение (13.2) в координатной форме представляется следующим образом
Каноническое:
Исключив t из уравнения (13.3), разрешив их сначала относи-тельно t, а затем, приравняв правые части равенств, имеем:
Если какая – либо координата направляющего вектора равна нулю, то равен нулю и числитель дроби.
25.Приведение общих уравнений прямой к каноническому виду
Пусть прямая задана общими уравнениями:
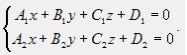
Если нужно привести ее уравнения к каноническому, то следует выбрать на этой прямой какую то точку и найти вектор, паралельный ей. Кординатами точки принадлежащей прямой, являеться любое из решений заданной линейной системы. Направляющим вектором прямой является вектор
нормальные векторы плоскостей задающих прямую.
