16.Полярные уравнения эллипса гиперболы и параболы

Полярное уравнение, общее по форме для эллипса, одной ветви гиперболы и параболы, имеет вид

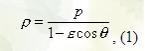
где

• полярные координаты произвольной точки линии, р - фокальный параметр (половина фокальной хорды линии, перпендикулярной к ее оси),   - эксцентриситет (в случае параболы  ). Полярная система координат при этом выбрана так, что полюс находится в фокусе, а полярная ось направлена по оси линии в сторону, противоположную ближайшей к этому фокусу директрисы.

17.Касательные к параболе, эллипсу, гиперболе

Касательная к параболе — это прямая, непараллельная оси параболы, имеющая с пара-

болой одну общую точку.

Пусть

-точка касания параболы

и прямой:

Имеем:

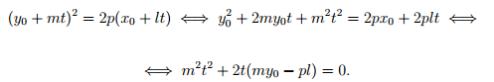
Это квадратное уравнение должно иметь один (двойной) корень, что возможно лишь

при выполнении условия

К аноническое уравнение касательной имеет вид

и окончательно

К асательная к эллипсу (гиперболе) — это прямая, имеющая с эллипсом (гиперболой)

одну общую точку.

Пусть

-точка касания эллипса.

и прямой

Имеем:

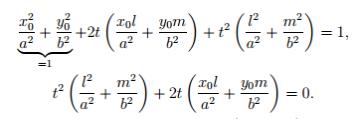
Это квадратное уравнение должно иметь один (двойной) корень, что возможно при

выполнении условия

так что можно положить

Каноническое уравнение касательной к эллипсу имеет вид

откуда, учитывая соотношение

п олучаем:

Аналогично получаем уравнение касательной к гиперболе

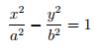
В точке

:

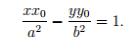
18.Общее уравнение плоскости

В декартовых координатах каждая плоскость определяется уравнением первой степени и каждое уравнение первой степени определяет плоскость.

Всякий (не равный нулю) вектор, перпендикулярный к данной плоскости, называется ее нормальным вектором. Уравнение

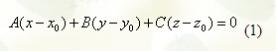
определяет плоскость, проходящую через точку

и имеющей нормальный вектор

Р аскрывая в уравнении (1) скобки и обозначая число

б уквой D, представим его в виде

Э то уравнение называется общим уравнением плоскости.

19.Неполные уравнения плоскости. Уравнение плоскости в отрезках.

Каждое уравнение первой степени

( в декартовых координатах) определяет плоскость. Если в этом уравнении отсутствует свободный член (D=0), то плоскость проходит через начало координат. Если отсутствует член с одной из текущих координат (то есть какой-либо из коэффициентов A, B, C равен нулю), то плоскость параллельна одной из координатных осей, именно той, которая одноименна с отсутствующей координатой; если, кроме того, отсутствует свобдный член, то плоскость проходит через эту ось. Если в уравнении отсутствуют два члена с текущими координатами (какие-либо два из коэффициентов A, B, C равны нулю), то плоскость параллельна одной из координатных плоскостей, именно той, которая проходит через оси, одноименные с отсутствующими координатами; если, кроме того, отсутствует свободный член, то плоскость совпадает с этой координатной плоскостью.

Если в уравнении плоскости

н и один из коэффициентов A, B, C не равен нулю, то это уравнение может быть преобразовано к виду

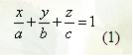
где

с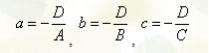 уть величины отрезков, которые плоскость отсекает на координатных осях (считая каждый от начала координат). Уравнение (1) называется уравнением плоскости «в отрезках».