14.Эксцентриситет эллипса и гиперболы. Эксцентриситет эллипса.

Определение. называется отношение c ⁄ a, где с — половина расстояния между фокусами, а — большая полуось эллипса.

Э ксцентриситет обозначают буквой ε: ε = c⁄ a. Так как ε = с ⁄ a, то 0 ≤ ε ≤ 1. Принимая во внимание, что :

Получим:

Из последнего равенства легко получается геометрическое истолкование эксцентриситета эллипса. При очень малом ε числа а и b почти равны, т.е. эллипс близок к окружности. Если же ε близко к единице, то число b весьма мало по сравнению с числом а и эллипс сильно вытянут вдоль большой оси. Таким образом, эксцентриситет эллипса характеризует меру вытянутости эллипса. Соотношения для фокальных радиусов для эллипса примут вид

Эксцентрисистет гиперболы

Определение.Эксцентриситетом гиперболы называется отношение с ⁄ а, где с — половина расстояния между фокусами, а — действительная полуось гиперболы.  Эксцентриситет гиперболы (как и эллипса) обозначим буквой ε. Так как с > а: то ε > 1, т. е. эксцентриситет гиперболы больше единицы. Очевидно,

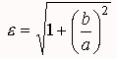
Из последнего равенства легко получается геометрическое истолкование эксцентриситета гиперболы. Чем меньше эксцентриситет, т. е. чем ближе он к единице, тем меньше отношение b ⁄a, а это означает, что основной прямоугольник более вытянут в направлении действительной оси. Таким образом, эксцентриситет гиперболы характеризует форму ее основного прямоугольника, а, значит, и форму самой гиперболы.  В случае равносторонней гиперболы ( a = b) имеем

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии а ⁄ ε от него, называются директрисами гиперболы (здесь а — действительная полуось, ε — эксцентриситет гиперболы).   Аналогично случаю эллипса доказывается теорема: если г — расстояние от произвольной точки М гиперболы до какого-нибудь фокуса, d — расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r ⁄ d есть величина постоянная, равная эксцентриситету гиперболы.  Установленное свойство эллипса и гиперболы можно положить в основу общего определения этих линий: множество точек, для которых отношение расстояний до фокуса и до соответствующей директрисы является величиной постоянной, равной ε , есть эллипс, если ε < 1, и гипербола, если ε > 1.

15.Директрисы Эллипса и Гиперболы

Директрисы Эллипса

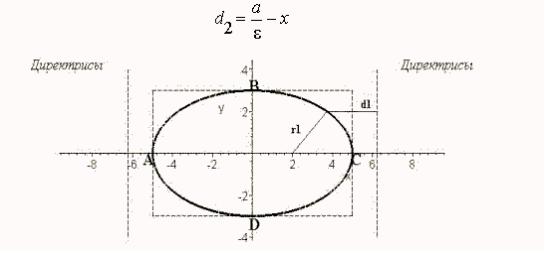Определение. Две прямые, перпендикулярные большой оси эллипса и расположенные симметрично относительно центра на расстоянии а⁄ ε от него, называются директрисами эллипса (здесь, а — большая полуось, ε — эксцентриситет эллипса). Так как для эллипса ε < 1, то a ⁄ ε > a. Отсюда следует, что правая директриса расположена правее правой вершины эллипса, а левая — общее свойство, присущее эллипсу. Теорема. Если r1 — фокальное расстояние произвольной точки М эллипса до какого-нибудь фокуса, d — расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r1 ⁄d есть постоянная величина, равная эксцентриситету эллипса. Д о к а з а т е л ь с т в о. Предположим для определенности, что речь идет о правом фокусе F1 и правой директрисе. Пусть М (х; у) — произвольная точка эллипса. Расстояние от точки М до правой директрисы выражается равенством

Кроме того,

С оставляя отношение, получим :

А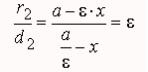 налогично доказывается для левого фокуса эллипса.

Директрисы Гиперболы

Определение. Директрисами гиперболы называются две прямые,уравнения которых в канонической для гиперболы системе координат имеют вид

Т ак как

О бозначение.Расстояние между директрисами обозначается 2d и равно

Теорема. Для любой точки гиперболы отношение ее фокального радиуса к расстоянию до соответствующей директрисы есть величина постоянная равная эксцентриситету:

Доказательство. При выводе канонического уравнения гиперболы мы получили формулы для вычисления фокальных радиусов точки гиперболы с координатами М(х, у):

где числа х, εx+a и εx-a иимеют одинаковые знаки. Из рисунка мы видим, что при х < 0

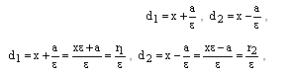
Теорема доказана.