
- •50)Второй замечательный предел
- •51) Непрерывность функции на отрезке
- •52) Классификация точек разрыва функции
- •Свойства Локальные
- •]Глобальные
- •Геометрический и физический смысл производной Тангенс угла наклона касательной прямой
- •Скорость изменения функции
- •57) Производные: постоянной, суммы, произведения, частного
- •Доказательство
- •Доказательство
- •58) Производная произведения функций.
50)Второй замечательный предел
![]() или
или ![]()
Следствия
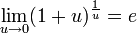
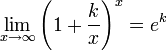
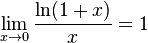
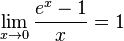
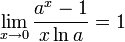 для
для 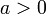 ,
, 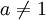
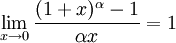
51) Непрерывность функции на отрезке
Наряду с непрерывностью функции в точке рассматривают ее непрерывность на разных промежутках.
Функция f(x) называется непрерывной на интервале (a, b), если она непрерывна в каждой точке этого интервала.
Функция f(x) называется непрерывной на отрезке [a, b], если она непрерывна на интервале (a, b), непрерывна справа в точке a и непрерывна слева в точкеb.
Свойства функций, непрерывных на отрезке
Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое число C> 0, что x [a, b] выполняется неравенство |f(x)| ≤ C.
Теорема 2 (Вейерштрасс). Если функция f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке своего наибольшего значения M и наименьшего значения m, т.е. существуют точки α, β [a, b] такие, что m = f(α) ≤ f(x) ≤ f(β) = M для всех x [a, b]
Теорема 4 (Больцано–Коши). Если функция f(x) непрерывна на отрезке [a, b], то она принимает на (a,b) все промежуточные значения между f(a) и f(b).
Cуществование непрерывной обратной функции
Пусть функция y = f(x) определена, строго монотонна и непрерывна на отрезке [a,b]. Тогда на отрезке [α, β] ( α = f(a), β = f(b) ) cуществует обратная функция x =g(y), также строго монотонная и непрерывная на отрезке (α, β).
52) Классификация точек разрыва функции
Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
Существуют левосторонний предел
 и
правосторонний предел
и
правосторонний предел 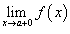 ;
;Эти односторонние пределы конечны.
При этом возможно следующие два случая:
Левосторонний предел и правосторонний предел равны друг другу:
![]()
Такая точка называется точкой устранимого разрыва.
Левосторонний предел и правосторонний предел не равны друг другу:
![]()
Такая
точка называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов![]() называется скачком
функции.
называется скачком
функции.
Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности.
53) Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.
Свойства Локальные
Функция, непрерывная в точке
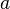 ,
является ограниченной в некоторой
окрестности этой точки.
,
является ограниченной в некоторой
окрестности этой точки.Если функция
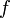 непрерывна
в точке
и
непрерывна
в точке
и 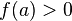 (или
(или 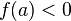 ),
то
),
то 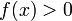 (или
(или 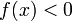 )
для всех
)
для всех 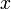 ,
достаточно близких к
,
достаточно близких к 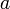 .
.Если функции и
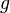 непрерывны
в точке
,
то функции
непрерывны
в точке
,
то функции 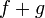 и
и 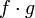 тоже
непрерывны в точке
.
тоже
непрерывны в точке
.Если функции и непрерывны в точке и при этом
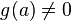 ,
то функция
,
то функция 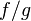 тоже
непрерывна в точке
.
тоже
непрерывна в точке
.Если функция непрерывна в точке и функция непрерывна в точке
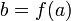 ,
то их композиция
,
то их композиция 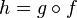 непрерывна
в точке
.
непрерывна
в точке
.
