14. Вектор поляризации и его связь с поляризационными зарядами

При поляризации диэлектрика каждая его молекула превращается в электрич. диполь, и приобретает опред. электрич. момент: 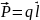( напр. от (-) к (+).

Д ля количеств. хар-ки поляризации диэл-ка служит физич. вел.– вектор поляризации – электрич.момент единицы объема диэлектрика.

Если диэл-ик однороден и смещ.зарядов одинак. во всех точках, то и вектор Р будет одинаков по всему диэл-ку.Такую поляризацию наз.однородной.

З ная вектор поляризации, можно опред. поляризационные заряды. Считаем поляризацию однородной. Рассм. в электрич.поле кусок диэл-ка в виде наклонной призмы с основанием S и ребром L׀׀ .

Если α–угол между направлением нормали к основанию призмы и , то объем призмы .

; p = Pτ

Сравнивая оба равенства

– проекция вектора Р на направление внешней нормали к рассматриваемой поверхности.

угол острый

угол тупой

9. Дифференциальная формулировка потенциальности электростатического поля

Е сли известно распред. потенц., то можно найти напр-ть этого поля в каждой точке. Рассм. в однор.поле 2е точки 1 и 2 и предп., что заряд +1 из точки 1 переходит в точку 2 вдоль отрезка .

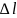– проекция напр-ти Е на направл. .

Введем теперь приращение потенц. при перемещ. , т. е. разность потенциалов в точке 2 и точке 1 и будем обозначать его просто , тогда , , .

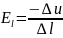Физич. смысл выраж. след.:напр-ть поля измеряется уменьш. потенциала,приходящ. на ед. длины вдоль линии напр-ти. Связь между нап-тью поля и потенциалом можно выразить с пом.понятия градиента потенциала. Градиентом люб. скалярный вел. φ в векторном анализе наз.вектор, напр. кот. совпад. с направл. быстрейшего увелич.велич. φ. Величина же этого вектора= измен.φ при перемещ. на ед. длины в направл. быстрейшего изменения.

Введем единич. вектор , совпад. с направл. линии напр-ти, тогда векторное знач. Е выраж.: , т. е. напр-ть электрост. поля = градиенту потенциала с обратным знаком: E = - grad φ

В случае неоднородного поля имеем

В ывод: распред. потенциалов в простр-ве однозначно опред. поле вектора . В этом смысле электрост. поле часто наз. потенциальным полем. Одним из хар-ых св-тв потенц. поля явл.равенство нулю циркуляции напряженности этого поля.

10. Поле диполя

Система из 2х точечн. зарядов +q и –q, находящ. на расст. друг от друга, наз. диполем. Такую систему в физике рассм. потому, что центры положит. и отриц. зарядов молекул многих в-тв можно представить смещен. друг относит.друга. Представл. о диполях часто позволяет с известным приближ. описать воздействие молекул различных в-тв. Модель дипольного сост.вещ-ва лежит в основе диэлектриков.Произведение полож. заряда на расст. между зарядами наз. моментом диполя: P=

Если расст. вектор, направл. от (-) к (+), то .

Рассм. жесткие диполи. Согласно принципа суперпозиции

Пусть точка набл.выбрана так,что длина . ; ,

α-угол между напр. момента диполя и направлением к точке наблюдения, проведенным из диполя.

Зная зав-ть потенциала от координат, можно найти напр-ть. Пользуемся полярными координатами r и α. ;

Полная напряженность в точке наблюдения равна:

Если α=0 или α=π, то

Эта формула выражает напряженность поля для точек, лежащих на линии момента диполя.

Если или , то

Эта формула определяет напряженность поля по линии, перпендикулярной к моменту диполя.