Модуль объемной деформации и модуль сдвига

В общем случае при решении плоской и пространственной задач любую деформацию грунта часто представляют в виде суммы объемных деформаций и деформаций сдвига. При этом используются следующие деформационные характеристики грунта:

• модуль объемной деформации ;

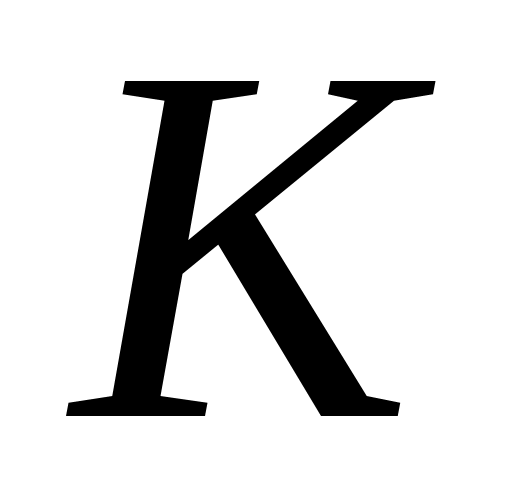• модуль сдвига .

Представим уравнение (2.6) в виде:

, (2.25)

где .

Добавляя в уравнение (2.25) с разными знаками соотношение , можно получить:

. (2.26)

Проводя аналогичные преобразования, получим уравнения для компонент и :

; (2.27)

. (2.28)

Первые слагаемые в уравнениях (2.26)-(2.27) характеризуют деформации сдвига (формоизменения объема грунта), а вторые – объемные деформации. Вводя обозначения для модуля объемного сжатия и модуля сдвига , преобразуем уравнения (2.26)-(2.28) к виду:

. (2.29)

; (2.30)

, (2.31)

где ; .

Коэффициент Пуассона связан с модулем объемного сжатия и модуля сдвига соотношением:

. (2.32)

Принцип гидроемкости грунта

Н.М. Герсевановым при рассмотрении общего случая объемной деформации введено допущение о том, что коэффициент пористости грунта зависит только от суммы нормальных напряжений и не зависит от их соотношения.

; (2.33)

. (2.34)

Для случая компрессионного сжатия это следует из следующих соотношений:

; (2.35)

; (2.36)

или в приращениях

. (2.37)

Подставляя в формулу (2.37), получим формулу

, (2.38)

в соответствии с которой, в случае компрессионного сжатия уменьшение пористости грунта в данной точке может произойти только при соответствующем увеличении суммы нормальных напряжений в этой точке.

Сделанное Н.М. Герсевановым допущение используется для расчета скорости уплотнения (консолидации) полностью водонасыщенного грунта, пористость которого связана с его влажностью. Поэтому условие (2.38) получило название принципа гидроемкости грунта.

Водопроницаемость грунтов

Водопроницаемостью называется свойство водонасыщенного грунта под действием разности напоров пропускать через свои поры сплошной поток воды. Водопроницаемость грунтов зависит от их пористости, гранулометрического и минералогического составов, градиента напора.

Уплотнение водонасыщенного грунта вызывает уменьше­ние его пористости и влажности за счет выдавливания воды из пор грунта. Очевидно, что процессы уплотнения и развития осадок грунтового основания зависят от скорости фильтрации воды. Законы филь­трации воды в грунтах необходимо знать также при определении притока воды в котлован, размеров воронки депрессии поверхности под­земных вод и т. п.).

Закон ламинарной фильтрации

Исследованиями установлено, что движение воды в порах грунта происходит в соответствии с законом ламинарной фильтрации. Математическое выражение этого закона, предложенное французским ученым Дарси (1854 г.), имеет вид:

, (2.39)

где – скорость фильтрации, или объем воды, проходящей через единицу площади поперечного сечения грунта в единицу времени; – коэффициент фильтрации, равный скорости фильтрации при гидравлическом градиенте ; – гидравлический градиент, равный потере напора , отнесенной к пути фильтрации :

. (2.40)

В соответствии с законом Дарси: скорость фильтрации прямо пропорциональна гидравличе­скому градиенту .

Коэффициент фильтрации является основной фильтрационной характеристикой грунтов и имеет размерность см/с или м/сут. Для различных грунтов значение коэффициента пористости зависит от плотности сложения, гранулометрического, минералогического составов и других факторов. Для песчаных грунтов его значение изменяется в пределах – ; для супесей – ; для суглинков – ; для глин – см/с, где может быть любым числом от 1 до 10.

Движение воды в песчаных грунтах происходит по закону лами­нарной фильтрации (кривая 1 на рис. 2.8). В порах плотного пылевато-глинистого грунта нет свободной воды или она находится в разобщенных между собой относительно крупных по­рах, в виде гидратных оболочек связанной воды, окру­жающих частицы грунта. При этом фильтрация воды начинается лишь при градиенте, большем некоторого значения, необходимого для пре­одоления сопротивления ее движению водно-коллоидных пле­нок (кривая 2 на рис. 2.8).

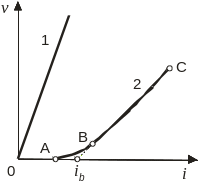
Рис. 2.8. График зависимости скорости фильтрации от градиента напора:

1 – для песка; 2 – для глины

На этой кривой можно выделить два основных уча­стка: криволинейный участок АВ, соответствующий переходу от момента возникновения фильтрации к моменту развития установившейся фильтрации, и участок установившейся фильтра­ции ВС.

Для участка ВС скорость фильтрации находят по выра­жению:

, (2.41)

где – коэффициент фильтрации, определяемый в интервале зависимости между точками В и С; – начальный градиент напора, определяемый по графику на рис. 2.8.

В водонасыщенных грунтах, обладающих начальным гради­ентом напора фильтрации воды в зоне с не­большими градиентами практически не происходит, поэтому при сложившемся напряженном состоянии грунт в этой зоне не сможет уплотняться по закону фильтрационной консолидации.

В лабораторных условиях коэффициент фильтрации песчаных грунтов определяют при постоянном заданном градиенте напора с пропуском воды сверху вниз или снизу вверх, при предварительном насыщении образца грунта водой снизу вверх. Коэффициент фильтрации пылеватых и глинистых грунтов определяют при заданном давлении на грунт и переменном градиенте напора с пропуском воды сверху вниз или снизу вверх, при предварительном насыщении образца грунта водой снизу вверх без возможности его набухания.

Коэф­фициент фильтрации песков и супесей для расчета притока воды в котлованы рекомендуется определять в полевых усло­виях методом пробных откачек или путем налива воды в сква­жины.