Закон уплотнения и линейная деформируемость грунта

Линейное уравнение (2.8) приближенно описывает изменение коэффициента пористости от давления в пределах ограниченного участка АВ компрессионной кривой (рис. 2.3, а). Для большого диапазона изменения давления компрессионная кривая первичного сжатия может быть описана зави­симостью, предложенной К.Терцаги

, (2.11)

где – коэффициент пористости при напряжении ; – начальный коэффи­циент пористости грунта; – коэффициент компрессии (параметр кривой); – давление, при котором начинается первичное сжатие грунта.

Выражение (2.11) в приращениях имеет вид:

, (2.12)

где – постоянная величина.

В соответствии с (2.12) при первичном сжатии изменение коэффици­ента пористости грунта прямо пропорционально изменению напряжений и обратно пропорционально суммарному напряжению. Эту зависимость применяют при рассмотрении деформации очень слабых грунтов, либо при изменении напряжений в значи­тельных пределах.

Линейная деформируемость грунта в пределах небольших изменений сжимающих напряжений вытекает из выражения (2.10):

. (2.13)

Так как для определенного грунта и выбранного интервала изменения сжимающих напряжений величина , то относительная деформация грунта прямо пропорциональна сжимающему напряжению . Следователь­но, грунт можно приближенно считать линейно деформируемым телом.

При изменении напряжений в значи­тельных пределах необходимо учитывать нелинейный характер зависимости между напряжениями и деформациями.

Компрессионная зависимость при объемном сжатии

При проведении компрессионных испытаний в одометрах об­разец грунта, находясь в жестком кольце, не имеет возможности бокового расширения. При действии сжимающего напряжения, равного ( – вертикальная сила, передаваемая на образец; – площадь поперечного сечения образца) на стенки кольца передаются горизон­тальные давления. В условиях отсутствия бо­кового расширения грунта, когда относительные горизон­тальные деформации = , горизонтальные на­пряжения = во внимание не принимались.

В общем случае они также будут оказывать влияние на деформируемость элементарного объема грунта в массиве. Для описания деформируемости грунта как линейно деформируемой среды можно использовать уравнения обобщенного закона Гука.

При действии на поверхности основания равномерно распределенной нагрузки (случай компрессионного сжатия) площадки, к которым приложены нормальные напряжения , , , будут главными, а касательные напряжения . В соответствии с законом Гука соотношения для компонент относительных деформаций имеют вид:

; (2.14)

; (2.15)

, (2.16)

где – коэффициент Пуассона, равный отношению величин поперечных и продольных деформаций образца при одноосном сжатии без ограничения бокового расширения:

. (2.17)

Для условий компрессионных испытаний в одометре, когда = , горизонтальные на­пряжения в соответствии с (2.15), (2.16) будут равны:

= = . (2.18)

По аналогии с коэффициентом бокового расширения грунта используется понятие коэффициента бокового давления грунта в состоянии покоя, равного отношению абсолютных значений нормальных напряжений, действующих на горизонтальных и вертикальных площадках элементарного объема грунта в условиях невозможности его бокового расширения:

. (2.19)

Коэффициенты бокового давления грунта и бокового расширения связаны между собой соотношениями:

; . (2.20)

Если при проведении компрессионных испытаний образца грунта имеется возможность измерить горизонтальные напряжения, возникающие при приложении к нему вертикального напряжения, то можно определить коэффициенты бокового давления и расширения грунта. Такие исследования выполняются в специальных приборах трехосного сжатия (стабилометрах) (рис. 2.5).

По данным Н.А. Цытовича, коэффициенты бокового давления и соответствующие им коэффициенты бокового расширения грунта могут находиться в пределах:

• для песчаных грунтов 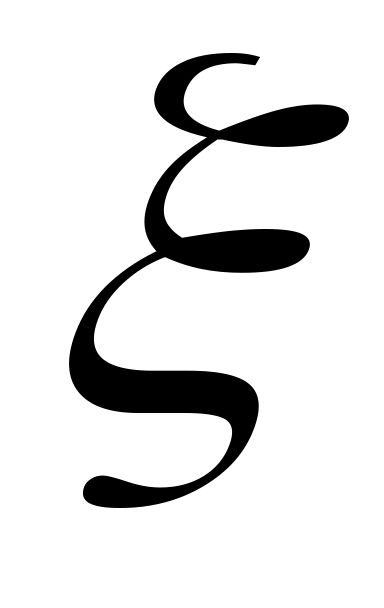=0,25–0,37; =0,2–0,27;

• для глинистых грунтов =0,1–0,82; =0,1–0,45.

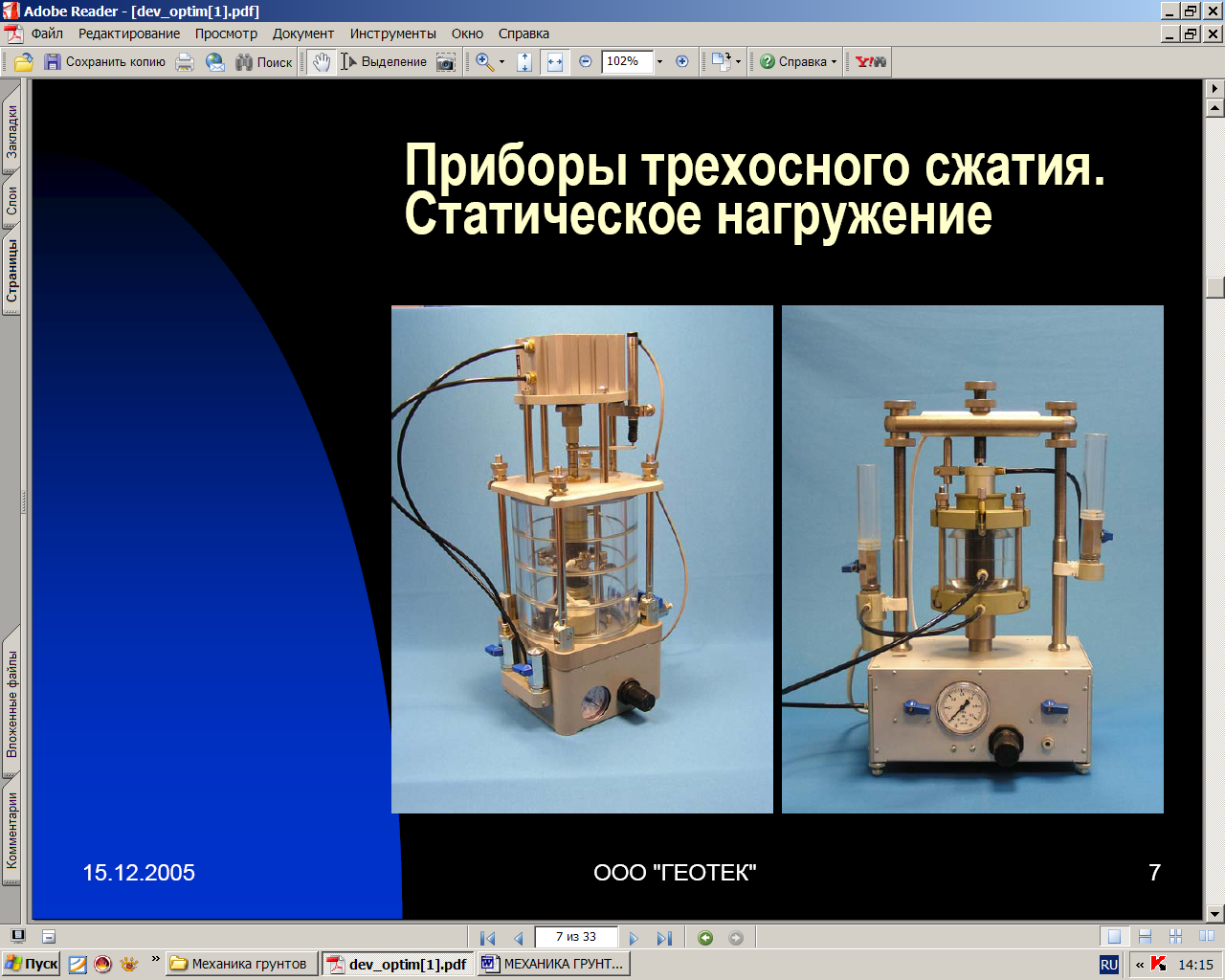
Рис. 2.4. Приборы трехосного сжатия для статического

нагружения фирмы «ГЕОТЕК»

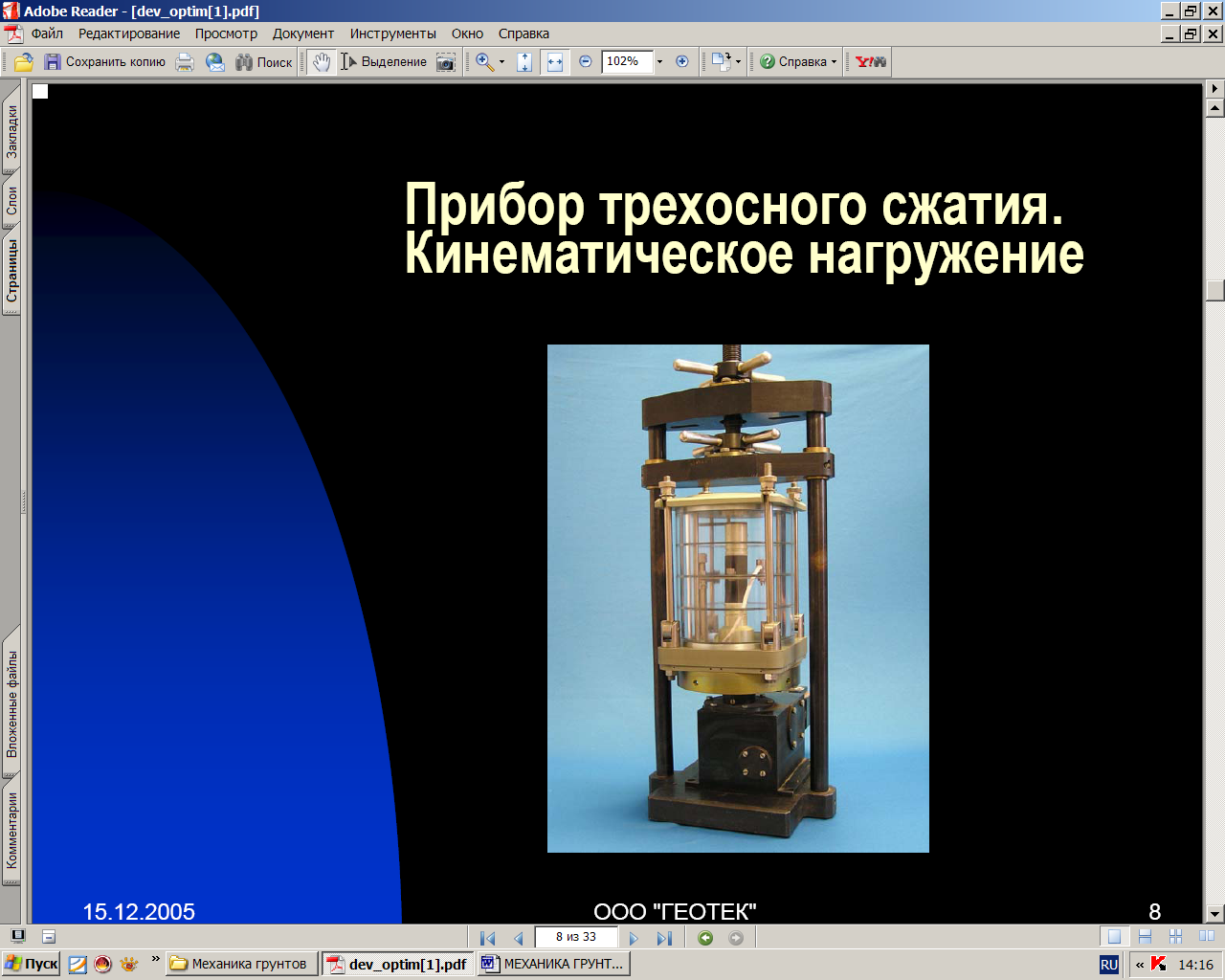
Рис. 2.5. Приборы трехосного сжатия с кинематическим

нагружением фирмы «ГЕОТЕК»

Подставляя в уравнение (2.8) значения = из формулы (2.18), можно получить:

, (2.21)

где - коэффициент, зависящий от или .