Ползучесть откосов и склонов
Прогнозирование деформаций ползучести откосов и склонов продиктовано необходимостью обеспечения нормальных условий эксплуатации сооружений, построенных на склонах.
Наиболее простой является реологическая модель Н.Н. Маслова вида:
,
(6.6)
где
-
коэффициент вязкопластического течения
при сдвиге (Па*с). Согласно этой модели
при
,
а при
.
Более
сложная реологическая модель учитывает,
что деформации в грунтах развиваются
и при
.
Поэтому начальный участок кривой
следует учитывать при составлении
реологического уравнения. Это можно сделать с помощью билинейной зависимости вида
,
(6.7)
где
-
коэффициент вязкого течения при сдвиге.
Ползучесть пласта в установившемся режиме
Для моделирования ползучести наклонного пласта при проникновении в него напорных волн в установившемся режиме необходимо рассматривать напряженно-деформированное состояние массива грунта под действием собственного веса, внешней нагрузки и внутренних источников напорных волн. В простейшем случае однородно-наклонного водонасыщенного пласта в установившемся режиме компоненты напряжений можно определять путем непосредственного интегрирования уравнений равновесия:
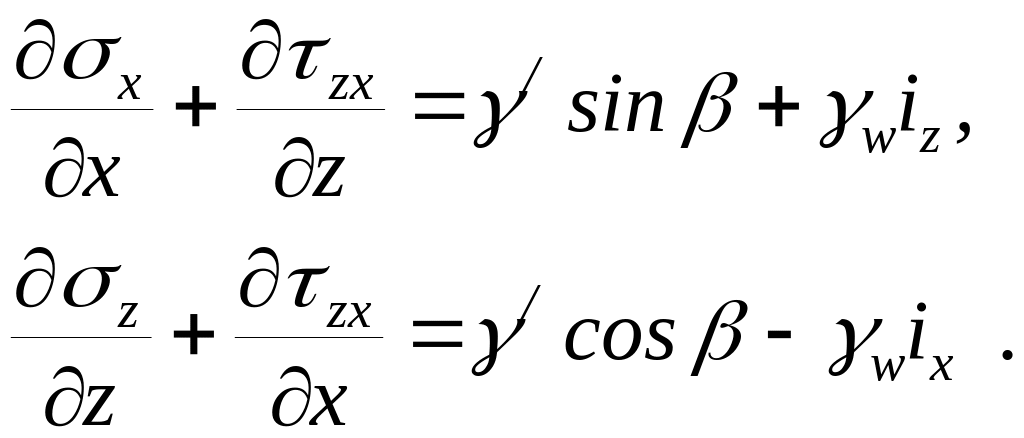
Так
как
,
то получим
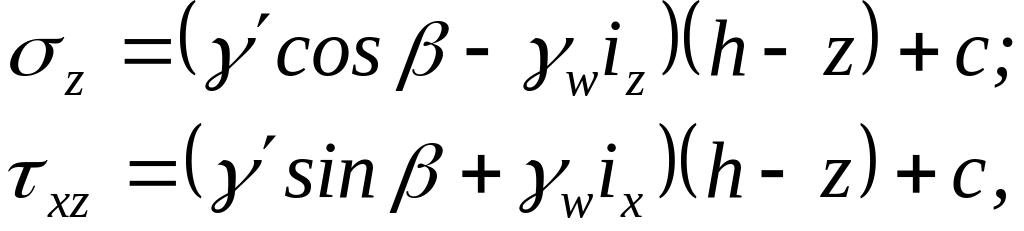(6.8)
где
-
угол наклона пласта;
-
компоненты гидравлического градиента;
-
удельные веса грунта (во взвешенном
состоянии) и воды соответственно; h
– мощность наклонного слоя. Учитывая,
что при z
= h
где р
– внешняя нагрузка, а также
,
вместо (6.8) получим:
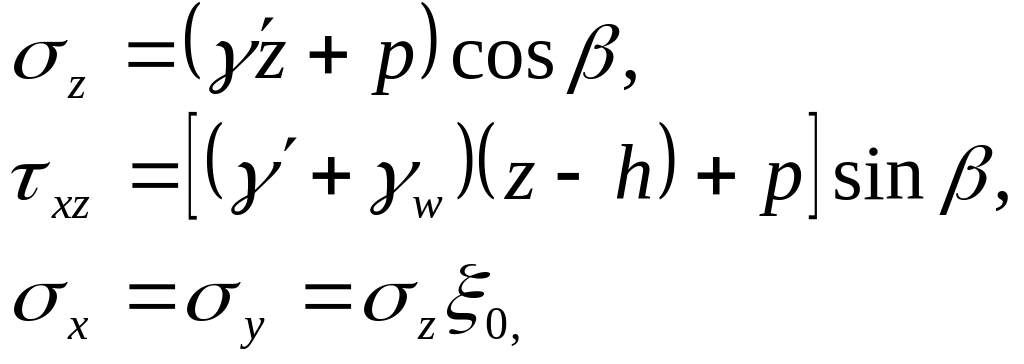
где
-
коэффициент бокового давления.
Подставляя
значения касательных напряжений в
реологическое уравнение состояния,
например (6.6) или (6.7), получим соответствующие
скорости угловой деформации
в любой точке наклонного пласта, по
которой можно построить эпюру изменения
скоростей смещения:
.
(6.9)
Известно, что при использовании уравнений состояния (6.6) эпюра скоростей смещения имеет параболическую форму, начиная с основания слоя, а, начиная с некоторых высот h*, слои жестко перемещаются вниз по склону на этом слое.
Если пласт опирается на трещиноватые водонасыщенные породы, в которых напор воды периодически меняется, то в глинистом пласте возникает неустановившийся режим напряженно-деформированного состояния, обусловливаемый проникновением напорных волн и влияющий в первую очередь на нормальные напряжения в скелете. Исследование вида эпюр скоростей оползневых смещений в наклонном пласте при неустановившемся режиме представляет отдельную задачу.
Давление грунтов на ограждающие конструкции
Ограждающие конструкции удерживают от обрушения находящийся за ними грунтовый массив. К ним относятся подпорные стены (массивные и гибкие), «стены в грунте», шпунтовые ограждения (рис. 7.1).
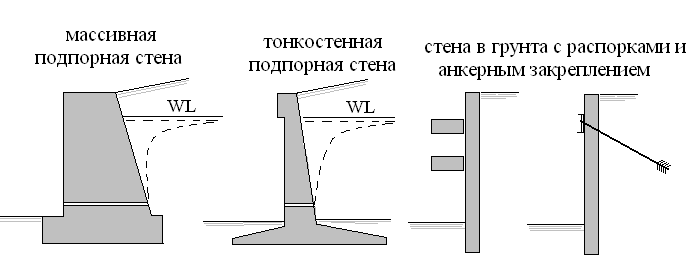
Рис. 7.1. Подпорные стены и шпунтовые ограждения
Устойчивость ограждающих конструкций обеспечивается как за счет собственного веса, так и за счет анкеров и распорок.
Взаимодействие ограждающей конструкции с массивом грунта имеет сложный характер и зависит от жесткости конструкции, от ее смещений и прогибов. При абсолютно неподвижном состоянии массива грунта за подпорной стеной реализуется так называемое давление покоя. При смещении стены от массива грунта за подпорной стеной реализуется активное давление. При движении стены на удерживаемый ею массив грунта в нем реализуется пассивное давление. Графически эти три вида давления представляются в виде зависимости
, (7.1)
где u – перемещение (рис. 7.2)
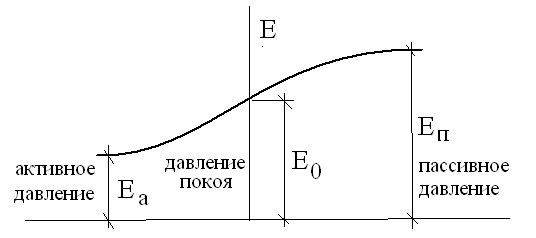
Рис. 7.2. Давления грунта на ограждающие конструкции