Области предельного напряженного состояния и условия их возникновения

Условие предельного равновесия Кулона-Мора, определяемое касательной к кругу, построенному на наибольшем и наименьшем главных напряжениях (рис. 5.4), никак не зависит от величины промежуточного главного напряжения . Это не позволяет в полной мере учесть пространственный характер напряженного состояния грунтовой среды. В действительности, как показывают эксперименты, промежуточное главное напряжение в ряде случаев влияет на прочность грунтов, например плотных песчаных и более крупнозернистых. Роль промежуточного главного напряжения учитывается в условии предельного равновесия Мизеса-Боткина. В этом условии А.И.Боткин обобщил для случая грунтовой среды теорию прочности Р. Мизеса, разработанную им применительно к металлам. При описании прочности грунтовой среды предлагается использовать систему октаэдрических площадок и соответствующих им октаэдрических напряжений (рис. 5.5).

Рис. 5.5. Октаэдрические площадки и напряжения

Октаэдрическими называются площадки, равнонаклоненные к координатным осям, совпадающим по направлению с направлением главных напряжений.

Октаэдрические напряжения, нормальное и касательное, выражаются по правилам, излагаемым в курсе сопротивления материалов, через главные напряжения

(5.6)

Условие предельного равновесия Мизеса-Боткина имеет следующий вид

(5.7)

или, учитывая (5.6)

, (5.8)

где - параметры прочности грунта (расчетные характеристики прочности) в модели Боткина.

Формула Пузыревского-Герсеванова

Для количественной оценки условий возникновения областей предельного напряженного состояния рассмотрим равномерную полосовую нагрузку q на основание от заглубленного в грунт сооружения (рис. 5.6).

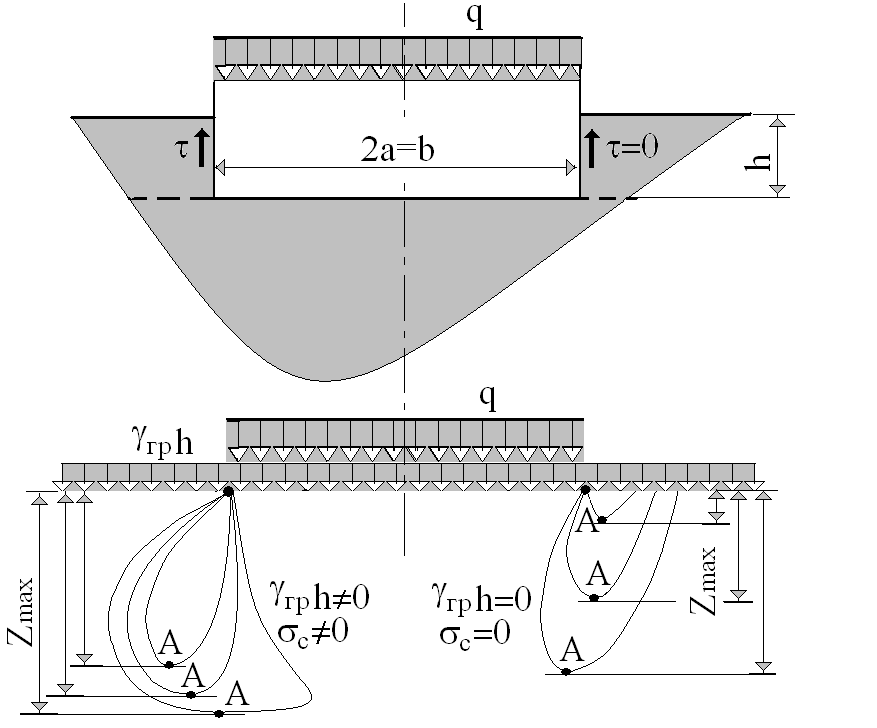
Рис. 5.6. Схема нагрузок на основание от сооружения

и развитие областей предельного равновесия

Полагаем, что нагрузка от сооружения q превосходит критическую краевую нагрузку , при которой под краями сооружения возникает предельное состояние. В условиях развития предельного состояния образуются области предельного напряженного состояния, которые распространяются на глубину (рис. 5.6). Задача определения условий возникновения областей предельного напряженного состояния сводится к нахождению связи интенсивности нагрузки q с координатой .

Решение этой задачи получено в рамках теории упругости Митчеллом с использованием системы координат, в которой координатами любой точки основания являются , где - угол видимости (рис. 5.7).

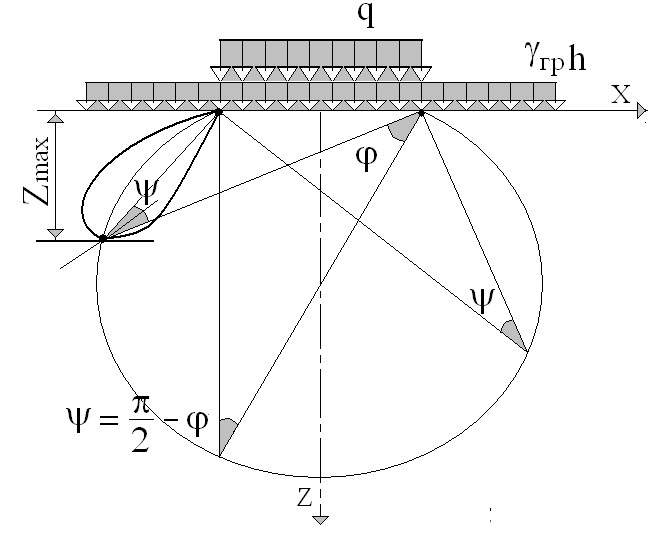
Рис. 5.7. Расчетная схема для вывода формулы Герсеванова-Пузыревского

Главные напряжения, возникающие от нагрузки , получены Митчеллом в виде:

.

Вертикальные и горизонтальные напряжения от собственного веса грунта определяются из соотношений:

;

(5.9)

.

В качестве допущения полагаем , что позволяет считать напряжения от собственного веса грунта одинаковыми по всем площадкам, в том числе и по направлению биссектрисы угла видимости. В этом случае суммарные напряжения в основании по главным площадкам будут:

;

.

С учетом напряжений от собственного веса грунта, синус наибольшего угла отклонения будет равен

.

Согласно условию предельного состояния в точках вне области предельного состояния . По мере приближения к ограничивающей кривой угол приближается к , а на самой кривой, ограничивающей область предельного равновесия, . Поэтому все точки ограничивающей кривой должны удовлетворять уравнению

. (5.10)

Это уравнение кривой, ограничивающей область предельного состояния грунта.

При движении вдоль горизонтальной прямой, проходящей через наиболее заглубленную точку этой кривой А с , величина изменяется вследствие изменения угла видимости. В точке касания А величина достигает своего максимума max , так как в этой точке, принадлежащей границе области предельного состояния , а в сколь угодно близких к ней справа и слева вдоль прямой , величина . Таким образом, при движении по линии и изменении угла видимости в точке А имеем max , что соответствует условию равенства нулю производной от по при :

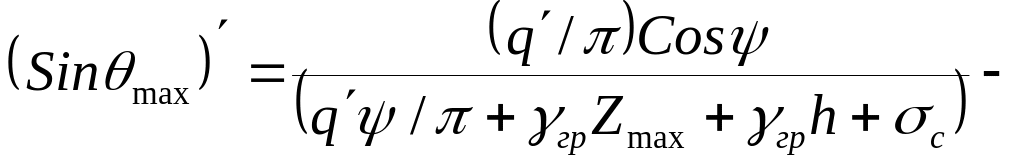
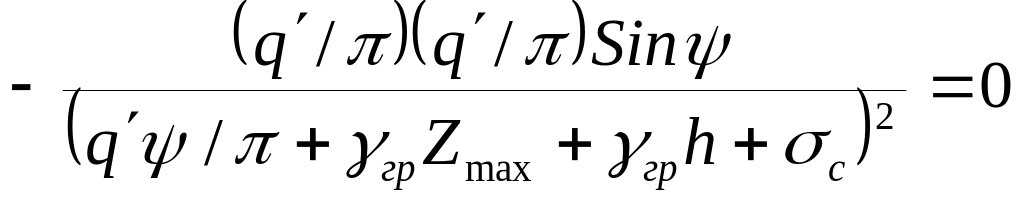
или

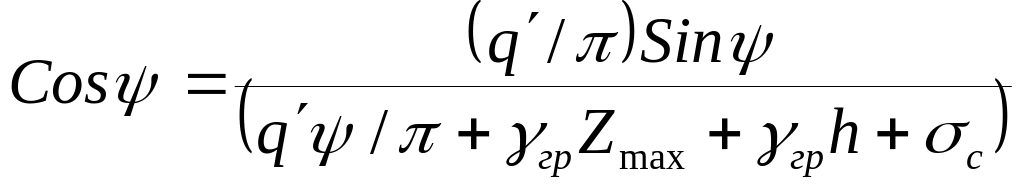. (5.11)

Сопоставляя условия (5.10) и (5.11) , получим

,

откуда в точке А .

Таким образом, для точки А имеем две координаты и . Подставляя их в (5.10), и учитывая что , получим

или, учитывая, что :

. (5.12)

Таким образом, получена зависимость между интенсивностью внешней нагрузки и глубиной распространения области предельного напряженного состояния.

Если в качестве условия принять = 0, то получим формулу Пузыревского-Герсеванова для критической краевой нагрузки:

. (5.13)

При этой нагрузке предельное напряженное состояние возникает только в точках под краями фундамента, а при меньшей нагрузке в основании нет областей предельного состояния.