Уравнения предельного равновесия

При определенном сочетании напряжений в грунте может возникнуть предельное равновесное напряженное состояние. Предельное напряженное состояние такое, при котором малейшее добавочное силовое воздействие или малейшее изменение прочности грунта приводит к нарушению существующего равновесия и потере устойчивости массива грунта.

В качестве основного условия предельного состояния принимают условие, сформулированное в 1773 г. Ш. Кулоном, связанное с возможностью начала скольжения одних масс грунта относительно других по площадкам, на которых действуют касательные и нормальные напряжения, связанные зависимостью (рис. 5.2)

, (5.1)

где и С – параметры линейной зависимости, условно называемые углом внутреннего трения и сцеплением. Для несвязных грунтов С=0.

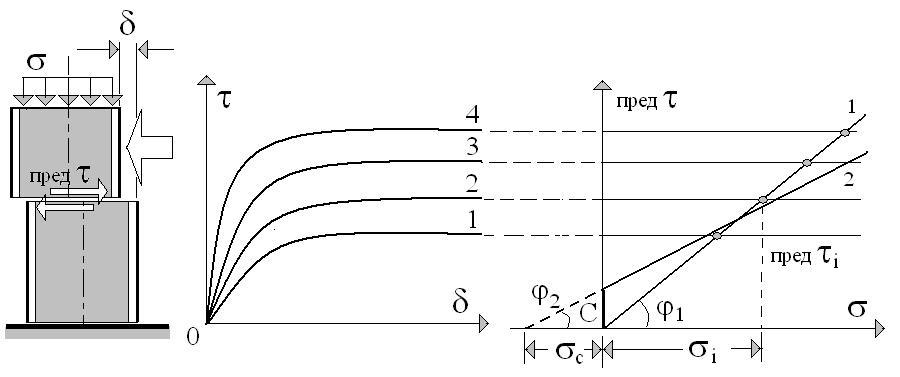
Рис. 5.2. Сопротивление сыпучих и связных глинистых грунтов сдвигу

В некоторых случаях удобно представлять условие предельного равновесия в форме

, (5.2)

где - напряжение всестороннего сжатия, эквивалентное связанности (фиктивная величина).

Зависимость Кулона для грунтов (5.1) является частным случаем появившейся позднее теории прочности Мора, где сопротивление сдвигу по какой-либо площадке является функцией нормального напряжения

. (5.3)

Угол наибольшего отклонения

В общем случае на любой элементарной площадке в грунтовой среде действуют касательные и нормальные (в том числе и фиктивное ) напряжения (рис. 5.3).

Равнодействующая этих напряжений называется полным приведенным напряжением. Оно отклоняется от нормали к площадке на угол . При повороте площадки этот угол меняется от _max до 0, при этом

. (5.4)

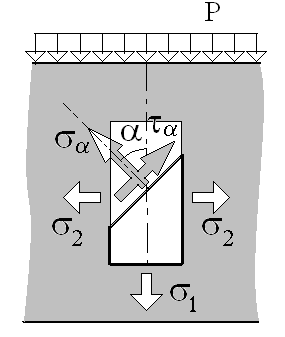
Рис. 5.3. Напряжения, действующие по элементарной площадке в грунтовой среде

Сопоставляя (5.2) и (5.4), видим, что состояние предельного равновесия будет достигнуто в данной точке при условии

. (5.5)

Таким образом, состояние предельного равновесия наступает тогда, когда максимальный угол отклонения полного приведенного напряжения от нормали к площадке становится равным углу внутреннего трения.

Диаграмма Мора

В условиях плоской задачи напряженное состояние описывается кругом (рис.5.4), построенным на разности главных напряжений _и₂ .

Любая точка на окружности соответствует площадке, наклоненной к главной площадке под углом и имеющей напряжения и (рис. 5.4). Угол наклона к оси прямой, проведенной в эту точку, будет углом отклонения полного приведенного напряжения от нормали к площадке . Наибольший угол отвечает точке касания прямой к кругу напряжений.

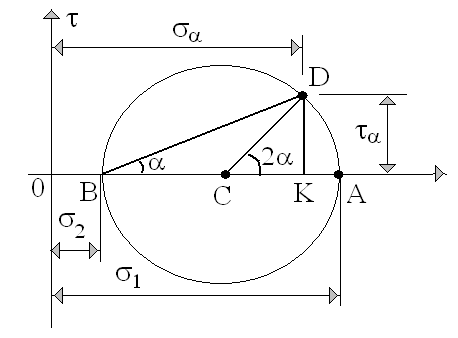
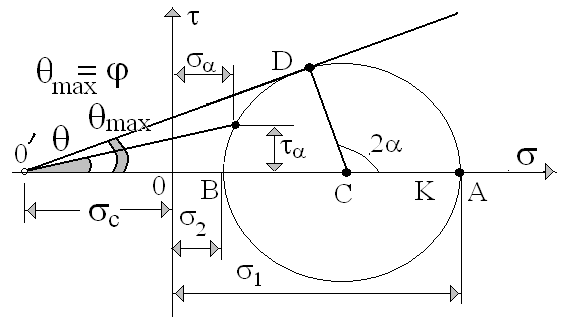
Рис. 5.4. Круг напряжений в условиях плоской задачи

Таким образом, учитывая условие (5.5), состояние предельного равновесия наступает только тогда, когда круг напряжений касается прямой, проведенной из точки под углом, равным углу внутреннего трения . Эта прямая называется предельной прямой.