Одномерная задача теории компрессионного уплотнения

Сжатие слоя грунта рассматривается в условиях невозможности бокового расширения при действии с поверхности безграничной по площади равномерно распределенной нагрузки. Ограниченной мощности слой сжимаемого грунта подстилается снизу скалистым основанием (рис. 4.1). В этом случае сжатие грунта будет аналогично сжатию в условиях компрессионных испытаний.

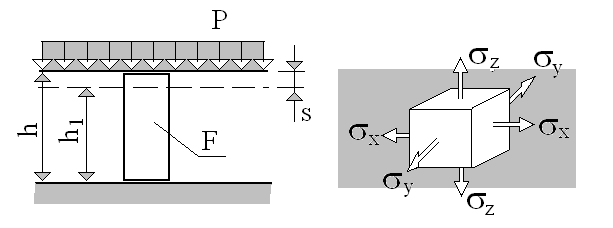
Рис. 4.1. Схема сжатия слоя грунта при сплошной нагрузке в условиях сжатия

без возможности бокового расширения

Из рисунка видно, что полная величина осадки

, (4.1)

где h – мощность сжимаемого слоя до обжатия его внешним давлением; h₁ – мощность сжимаемого слоя после обжатия.

Объем скелета грунта в единице объема грунта

.

Объем скелета в выделенной грунтовой массе в виде призмы площадью F до и после деформации остается постоянным

.

Из этого условия можно найти h₁

, (4.2)

где F – площадь грунтовой призмы; е₁ – коэффициент пористости грунта до приложения нагрузки; е₂ – коэффициент пористости грунта после окончания осадки под нагрузкой.

Подставляя (4.2) в (4.1), получаем

или

.

Из результатов компрессионных испытаний можно положить, что

,

где m₀ – коэффициент уплотнения (сжимаемости).

Тогда формула для величины конечной осадки примет вид

или

, (4.3)

где - коэффициент относительной сжимаемости, завися-щий только от компрессионных свойств грунта.

Таким образом, для вычисления величины осадки используются результаты компрессионных испытаний для оценки сжимаемости грунта и коэффициента уплотнения. Величину осадки можно также найти по результатам полевых испытаний, в которых определяется модуль общей деформации грунта Е₀.

При принятой схеме сжатия слоя грунта (рис. 4.1)

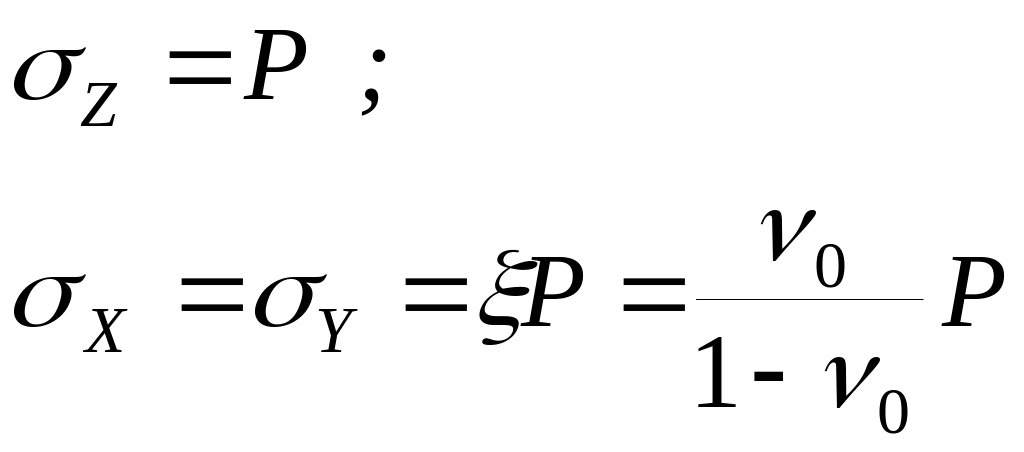, (4.4)

где - коэффициент бокового давления; - коэффициент бокового расширения.

Из курса сопротивления материалов следует, что относительная деформация грунта вдоль оси Z, совпадающей с направлением действия силы Р,

. (4.5)

Подставив (4.4) в (4.5), получим

,

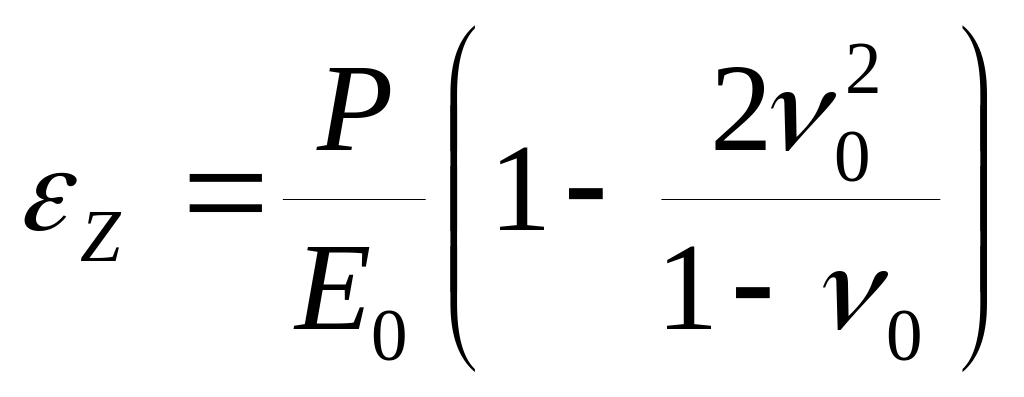или, вводя обозначение

,

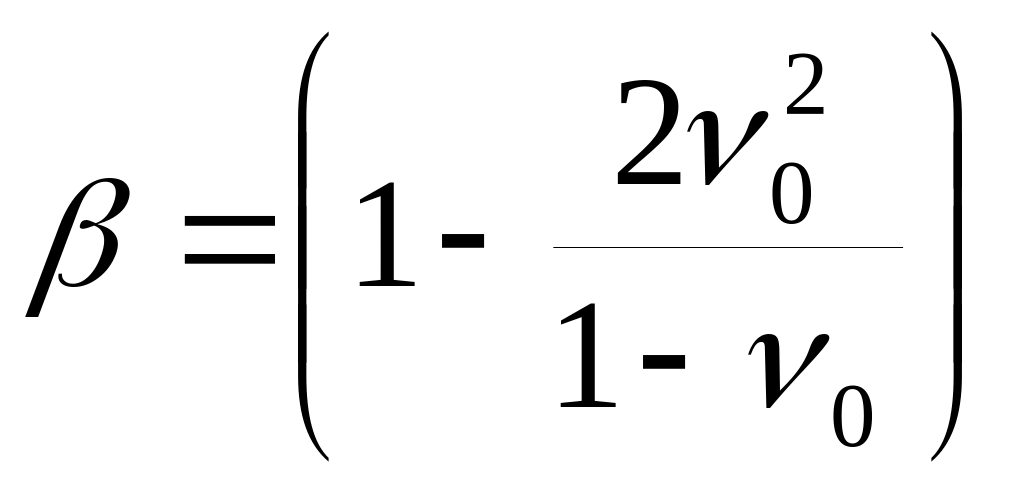получим

.

Полная величина осадки равна произведению относительной осадки на мощность деформируемого слоя

. (4.6)

Здесь - коэффициент, зависящий только от свойств грунта и вычисляемый на основе опытного определения коэффициента бокового давления или коэффициента бокового расширения .

Сравнивая (4.3) и (4.6), можно найти зависимость между и Е₀:

.

Отсюда следует

.

Данная зависимость устанавливает обратную пропорциональность величин Е₀ .

Метод эквивалентного слоя

Эквивалентным слоем грунта называется слой, осадка которого при сплошной нагрузке равна осадке фундамента на мощном массиве при местной нагрузке на полупространстве:

. (4.7)

При сплошной нагрузке относительная деформация слоя грунта

.

Отсюда следует

. (4.8)

С другой стороны, осадка реального фундамента на мощном массиве грунта или слое грунта ограниченной мощности

, (4.9)

где w – коэффициент формы и жесткости; b − ширина загруженной площади.

Подставляя в выражение (4.7) значения (4.8) и (4.9) и решая уравнения относительно h₀, получим

. (4.10)

Вводя обозначение

,

получим формулу для определения мощности эквивалентного слоя грунта

, (4.11)

где b − ширина фундамента.

Из формулы (4.11) видно, что мощность эквивалентного слоя грунта зависит от бокового расширения грунта (коэффициент А), от формы и жесткости фундамента (коэффициент w) и пропорциональна ширине фундамента.

С учетом (4.11) получим формулу для определения осадки фундамента заданных размеров

. (4.12)

Значения коэффициента эквивалентного слоя табулированы для определения максимальных и средних осадок гибких фундаментов ( , ) и осадок абсолютно жестких фундаментов ( ) в зависимости от отношения сторон фундамента l/b и коэффициента Пуассона v₀ . Следует отметить, что существуют следующие соотношения между коэффициентами:

• для круглых и квадратных фундаментов

;

• для центра прямоугольной площади абсолютно гибкой нагрузки и ее угловой точки

, (4.13)

где − коэффициент эквивалентного слоя для угловой точки.

Лекция № 6

Деформации грунтов и расчет осадок фундаментов. Метод послойного суммирования,

Изменение осадок во времени

Метод послойного суммирования

Метод послойного суммирования применяют при определении осадок фундаментов ограниченных размеров. Сущность данного метода состоит в следующем. При размерах фундаментов, значительно превышающих мощность сжимаемого слоя грунта, можно считать сжатие грунта происходящим без возможности бокового расширения

и воспользоваться для определения величины осадки приведенными ранее зависимостями (4.6), (4.12).

Границей применимости этих формул считают условие

,

где b − ширина меньшей стороны фундамента.

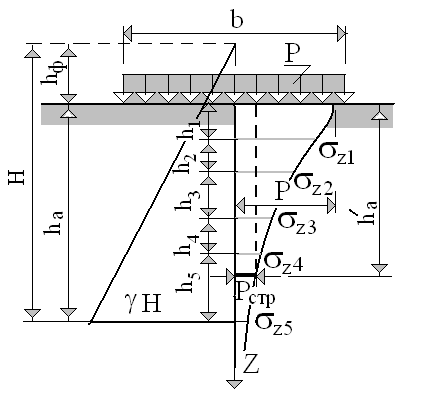
Рис. 4.2. Схема распределения вертикальных напряжений в линейно деформируемом полупространстве расчета осадок основания методом послойного суммирования

При нельзя пренебрегать затуханием вертикальных напряжений по глубине. Эти изменения будут тем значительнее, чем глубже расположен жесткий подстилающий слой.

Суть метода послойного суммирования состоит в том, что эпюру вертикальных напряжений (рис. 4.2) в основании по центральной оси фундамента разбивают на участки, соответствующие мощности отдельных слоев грунта , в пределах каждого элементарного слоя считают величину напряжений неизменной и равной величине среднего напряжения в рассматриваемом слое, т.е. заменяют действительную криволинейную эпюру ступенчатой.

В этом случае сжатие в пределах каждого слоя рассматривают как сжатие без возможности бокового расширения, а величину осадки определяют как сумму осадок отдельных слоев.

Для построения эпюры напряжений (рис. 4.2) пользуются таблицами значений коэффициента α, дающего возможность определить величину (давления по оси, проходящей через центр области нагружения на расстоянии z от поверхности грунта) в долях от величины внешней нагрузки .

Коэффициент α определяется в зависимости от отношения сторон фундамента l/b (где l − бóльшая из сторон фундамента) и отношения z/b. Таблицы значений α приведены в СНиП и справочниках. Тогда на любой глубине величина напряжения

.

Полная величина осадки может быть найдена как сумма осадок отдельных слоев

(4.14)

(4.15)

где или − величины осадок отдельного слоя грунта.

Для случая однородного основания характеристики грунта β, Е₀, m₀ можно считать неизменными, а мощность слоев принять одинаковой по глубине, тогда и выражения (4.14) и (4.15) примут вид:

(4.16)

(4.17)

При определении осадки фундамента необходимо учесть влияние глубины его заложения и установить пределы суммирования по глубине. Грунт, залегающий в уровне подошвы фундамента, до возведения сооружения уже был обжат давлением собственного веса вышележащего грунта, так называемым бытовым давлением. Поэтому для определения величины осадки фундамента начальную ординату давления на грунт принимают

,

где − дополнительное вертикальное давление на основание от сооружения (для фундаментов шириной b ³ 10 м принимается = ); − вертикальное напряжение от собственного веса грунта (бытовое давление) на уровне подошвы фундамента.

Последующие ординаты эпюры определяют по формуле

, (4.18)

где .

Чем глубже рассматриваемое сечение грунта от поверхности земли, тем больше величина бытового давления и тем меньше напряжения от сооружения. Суммирование осадок производят лишь в зоне действия существенных напряжений от сооружения. Эту зону называют сжимаемой толщей грунта, или активной (рабочей) зоной. Нижняя граница сжимаемой толщи грунта принимается на глубине , где выполняется условие:

.

Положение границы сжимаемой толщи может быть найдено графически: для этого проводят прямую, соединяющую ординаты 0,2 бытового давления; пересечение этой прямой с эпюрой σ_Z давлений от сооружения покажет положение границы сжимаемой толщи (прямая АВ).

Если найденная граница сжимаемой толщи находится в слое грунта с модулем деформации МПа, или такой слой залегает

непосредственно ниже глубины , нижняя граница сжимаемой толщи грунта принимается на глубине, где выполняется условие:

.

Мощность сжимаемой толщи зависит от ряда факторов. Она увеличивается при возрастании давления от сооружения р и увеличении размеров площади загружения и уменьшается с увеличением глубины заложения фундамента. На нее влияет форма фундамента (разное затухание напряжений по глубине), а также вид и состояние грунта (степень возрастания бытового давления по глубине).