Сопротивление сдвигу сыпучих грунтов

Для определения сопротивления сдвигу образец грунта испытывают в сдвиговом приборе в виде кольца, разрезанного по горизонтальной плоскости (рис. 2.10). Приложив силу F и постепенно увеличивая силу , можно достигнуть среза (сдвига) одной части образца по другой приблизительно по линии, обозначенной пунктиром. Прибор имеет нижнюю неподвижную обойму, верхнюю подвижную обойму и фильтрующие пластины сверху и снизу.

По измеренным в процессе испытания значениям касательной и нормальной нагрузок вычисляют касательные и нормальные напряжения и , по формулам:

; , (2.44)

где и – соответственно касательная и нормальная силы к плоскости среза; – площадь среза.

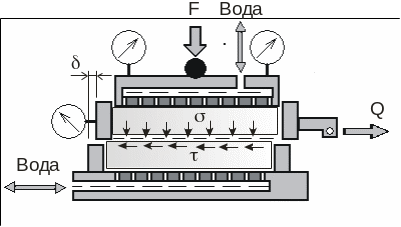
Рис. 2.10. Схема прибора одноплоскостного среза (сдвига)

Если провести несколько таких опытов при различном вертикальном напряжении , то можно построить график зависимости предельного сопро­тивления сыпучего грунта сдвигу от сжимающего напряжения (рис. 2.11).

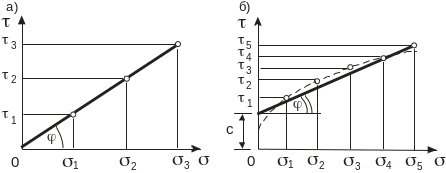
а) б)

Рис. 2.11. Графики со­противления сдвигу сыпучего (а) и связного (б) грунтов

В интервале изменения сжимающих напряжений 0–0,5 МПа (действующих в основании фундаментов промышленных и гражданских зданий) график зависимости касательных напряжений от вертикальных сжимающих напряжений с достаточной точностью может быть представлен в виде отрезка прямой, выходящей из начала координат (рис. 2.10, а). Зависимость может быть выражена уравнением:

, ( 2.45)

где – угол внутреннего трения; – коэффициент внутреннего трения, характеризующий трение грунта о грунт.

Зависимость (2.45) установлена Ш. Кулоном в 1773 г. и выражает закон сопротивления сыпучих грунтов сдвигу: предельное сопротивление сыпу­чих грунтов сдвигу прямо пропорционально нормальному на­пряжению. Этот закон называется законом Кулона.

Сопротивление сдвигу связных грунтов

Пылевато-глинистые грунты (глины, суглинки и супеси) обладают связностью, интен­сивность которой зависит от влажности грунта и степени его уплотненности. Приложенная к об­разцу водонасыщенного грунта вертикаль­ная нагрузка в первый момент времени передается на поровую воду. Лишь по мере выдавливания ее из пор это давление будет воздействовать на скелет грунта. В связи с этим обра­зцы грунта испытывают на сдвиг после консолидации грунта, когда нормальное напряжение уже передано на скелет грунта.

Если в сдвиговом приборе (рис. 2.10) провести несколько испытаний на сдвиг нескольких образцов одного и того же грунта, подвергая образцы воздействию различных напряжений , то получим криволинейную зависимость предельного сопротивления грунта сдвигу от (рис. 2.11, б). Криволинейность графика наиболее выражена при малых значениях . В интервале напряжений 0,05–0,5 МПа прак­тически имеем прямую, описываемую уравнением

, ( 2.46)

где – удельное сцепление пылевато-глинистого грунта, характеризующее его связность.

Зависимость (2.46) выражает закон сопротивления пылевато-глинистых грунтов сдвигу: предельное сопротивление связных грунтов сдвигу при завершенной их консолидации есть функция первой степени нормального напряжения.

Если прямую АВ продлить влево до пересечения с осью абсцисс, то она отсечет на ней отрезок :

. (2.47)

Эту величину, заменяющую действие всех сил сцепления, называют давлением связности. С учетом (2.47) уравнение (2.46) может быть представлено в виде:

. ( 2.48)

Соотношение (2.48) формально показывает, что проявление связности (сцепления) грунта как бы эквивалентно фиктивному увеличению нормального напряжения в плоскости сдвига, повышающему прочность грунта.

. ( 2.49)

Для оценки сопротивляемости грунтов сдвигу при не­полной их консолидации используют график с параметрами и , приведенный на рис. 2.11, б, но нормальное напряжение уменьшают на величину давления в поровой воде, то есть принимают рав­ным напряжению в скелете грунта:

, ( 2.50)

где – полное нормальное напряжение; –давление в поровой воде при неполной консолидации грунта.