4.2 Уравнение касательной к графику функции.

Составим уравнение касательной к графику функции при . Эта прямая должна проходить через точку с координатами (х₀,у₀), лежащую на графике функции, где у₀ = f(x₀), и иметь угловой коэффициент, равный производной при . Воспользовавшись уравнением прямой с угловым коэффициентом, получим: у = f`(x<sub>0</sub>)х + b, причем у<sub>0</sub> = f`(x₀)x₀ + b, то есть b = y₀ - f`(x₀)x₀. Тогда уравнение касательной можно записать в виде:

или (4.5)

Углом между двумя линиями называется угол между касательными к этим линиям, проведенными в точке пересечения линий. Следовательно, необходимо найти точку пересечения, затем производные от функции в этой точке и найти

(4.6)

4.3 Формула Тейлора с остаточным членом в форме Пеано и в форме Лагранжа

Рассмотрим функцию , имеющую в окрестности точки х=а все производные до порядка (n+1) включительно, и поставим задачу: найти многочлен y=P_n(x) степени не выше n, для которого его значение в точке а, а также значения его производных по n-й порядок равны значениям при x=a выбранной функции и ее производных соответствующего порядка:

(4.7)

Пусть искомый многочлен имеет вид:

P_n(x)=C₀+C₁(x-a)+C₂(x-a)²+…+C_n(x-a)ⁿ. (4.8)

При этом

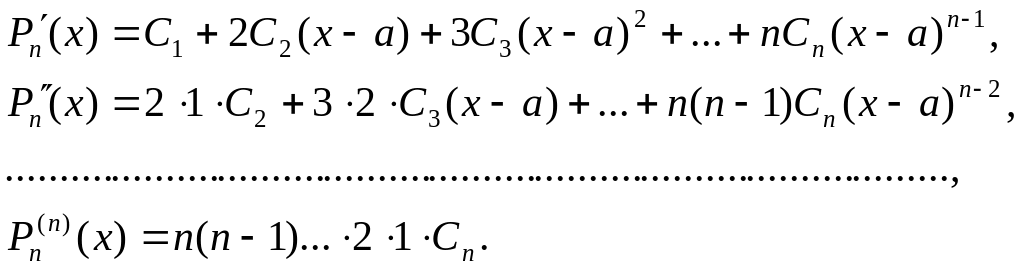
Тогда

(4.9)

Из формул (4.9) можно выразить коэффициенты С_i через значения производных данной функции в точке а.

Замечание. Произведение последовательных натуральных чисел 1∙2∙3∙…∙(n-1)n называется факториалом числа n и обозначается

n! = 1∙2∙3∙…∙(n-1)n . (4.10)

Дополнительно вводится 0!=1.

Используя это обозначение, получим:

(4.11)

Таким образом, искомый многочлен имеет вид:

(4.12)

Обозначим через R_n(x) разность значений данной функции f(x) и построенного многочлена P_n(x): R_n(x) = f(x) – P_n(x), откуда f(x) = P_n(x) + R_n(x) или

(4.13)

Полученное представление функции называется формулой Тейлора, а R_n(x) называется остаточным членом формулы Тейлора. Для тех значений х, для которых R_n(x) мало, многочлен P_n(x) дает приближенное представление функции . Следовательно, формула (4.13) дает возможность заменить функцию многочленом y = P_n(x) с соответствующей степенью точности, равной значению остаточного члена R_n(x).

Формы остаточного члена в формуле Тейлора

Покажем, что R_n(x) = o(x-a)ⁿ. Из выбора многочлена P_n(x) следует, что

Применив для вычисления предела n раз правило Лопиталя, получим:

. Утверждение доказано. Представление остаточного члена в виде

R_n = o(x-a)ⁿ (4.14)

называется записью остаточного члена в форме Пеано.

Найдем еще один вид записи R_n(x). Представим его в виде

(4.15)

и определим вид функции Q(x). Из (4.12) следует, что

. (4.16)

Пусть при заданных значениях х и а Q(x)=Q. Рассмотрим вспомогательную функцию от t ( ):

При этом предполагается, что а и х приняли фиксированные значения. Тогда

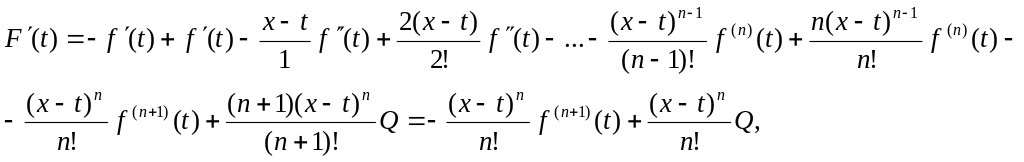
то есть F(t) дифференцируема в окрестности точки а. Из (4.16) следует, что F(x) = F(a) = 0, поэтому к функции F(t) можно применить теорему Ролля: существует t = ξ (a < ξ < x) такое, что F′(ξ) = 0. Тогда , откуда Q = f⁽ⁿ⁺¹⁾ (ξ). Подставив это выражение в формулу (21.9), получим запись остаточного члена в форме Лагранжа:

. (4.17)

Так как a < ξ < x, можно представить ξ = а + θ(х – а), где 0 < θ < 1. При этом

. (4.18)

Замечание. Если в формуле Тейлора принять а = 0, этот частный случай называют формулой Маклорена:

. (4.19)