
- •3 Дифференциальное исчисление 2
- •4 Применение производной 12
- •3 Дифференциальное исчисление
- •3.1 Производная функции, ее геометрический и механический смысл. Уравнение касательной к графику функции
- •3.2 Дифференцируемость функции. Дифференцируемость функции, ее связь с непрерывностью. Дифференциал функции, его геометрический смысл
- •3.3 Свойства производной (правила дифференцирования)
- •3.4 Производная сложной и обратной функций
- •3.5 Инвариантность формы дифференциала
- •3.6 Таблица производных
- •3.7 Метод логарифмическое дифференцирование. Производная показательно-степенной функции
- •3.8 Дифференцирование функций, заданных неявно и параметрически
- •3.9 Производные и дифференциалы высших порядков, их свойства
- •3.10 Точки экстремума функции. Теоремы Ферма и Ролля
- •3.11 Теоремы Лагранжа и Коши
- •4 Применение производной
- •4.1 Правило Лопиталя. Раскрытие неопределенностей.
- •4.2 Уравнение касательной к графику функции.
- •4.3 Формула Тейлора с остаточным членом в форме Пеано и в форме Лагранжа
- •4.4 Разложение основных элементарных функций по формуле Тейлора
- •4.5 Условия возрастания и убывания функции. Экстремумы функции, необходимое условие. Достаточные условия
- •4.6 Отыскание наибольшего и наименьшего значений функции, дифференцируемой на отрезке
- •4.7 Исследование выпуклости функции. Точки перегиба, их нахождение
- •4.8 Асимптоты функций
- •4.9 Общая схема исследования функции и построения ее графика
3.5 Инвариантность формы дифференциала
Найдем выражение для дифференциала сложной функции.
Пусть , , то есть .
Тогда
![]() следовательно,
следовательно,
![]()
Но
![]() поэтому
поэтому
![]() Таким образом, форма дифференциала не
зависит от того, является аргумент
функции независимой переменной или
функцией другого аргумента. Это свойство
называется свойством неизменности, или
инвариантности, дифференциала.
Таким образом, форма дифференциала не
зависит от того, является аргумент
функции независимой переменной или
функцией другого аргумента. Это свойство
называется свойством неизменности, или
инвариантности, дифференциала.
3.6 Таблица производных
Используя полученные формулы и свойства производных, найдем производные основных элементарных функций.
Если
 ,
то
,
то
 ,
поэтому
,
поэтому
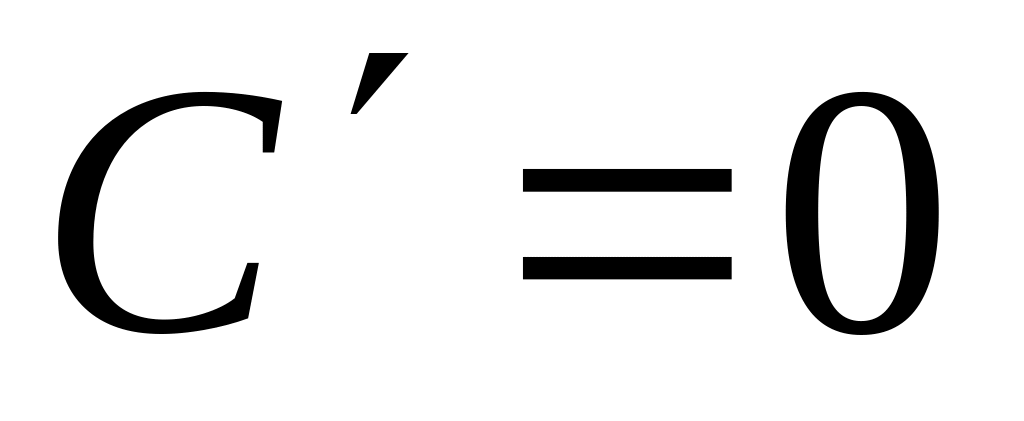 .
.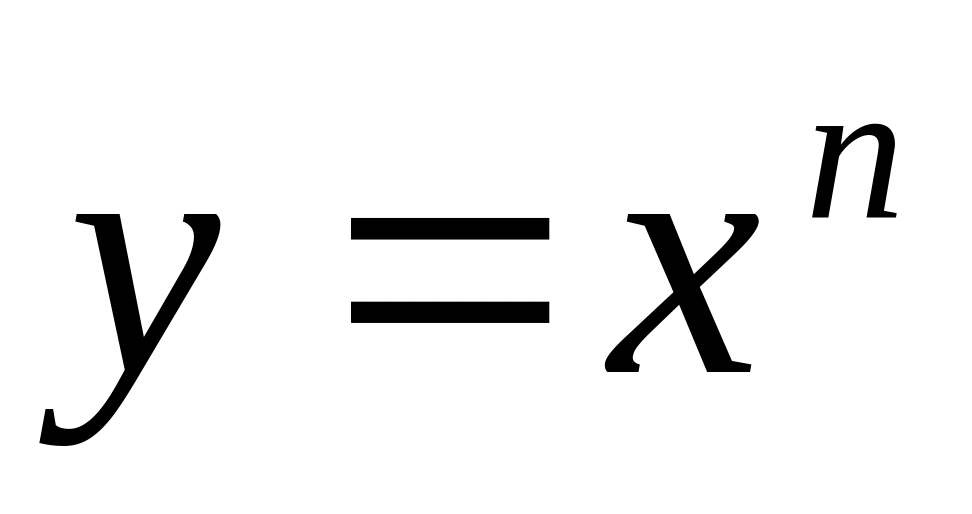 ,
где
,
где
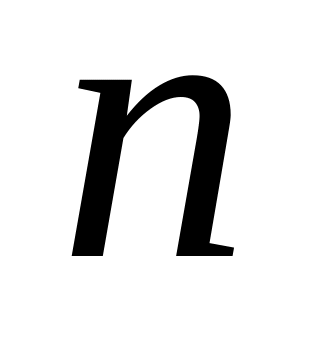 – натуральное число. Тогда по формуле
бинома Ньютона можно представить
– натуральное число. Тогда по формуле
бинома Ньютона можно представить
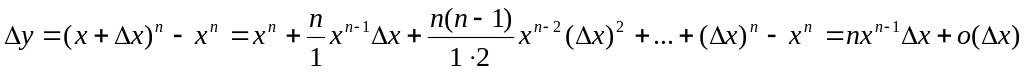 Следовательно,
Следовательно,
 .
.y = sinx,

y = cosx,

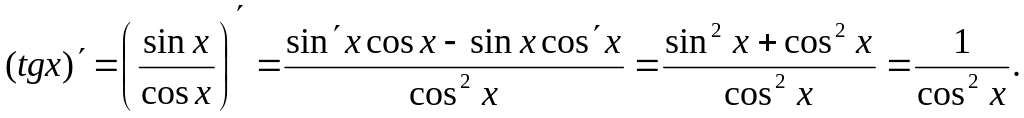
Аналогично можно получить формулу

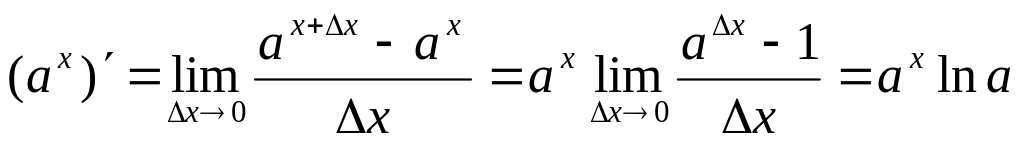 (см. 2-е следствие из второго замечательного
предела).
(см. 2-е следствие из второго замечательного
предела).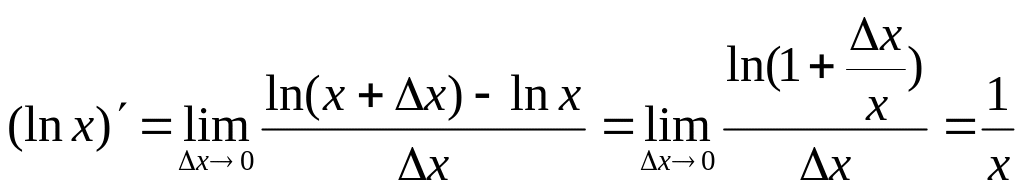 (см. 1-е следствие из второго замечательного
предела).
(см. 1-е следствие из второго замечательного
предела).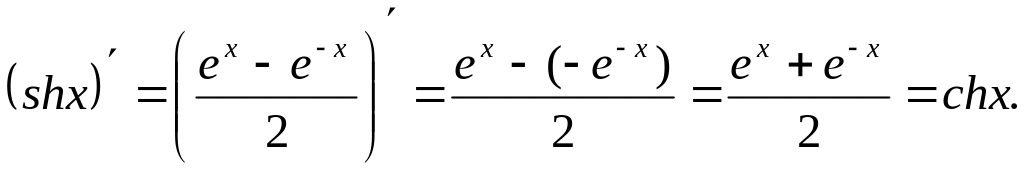 Таким же образом можно найти производные
остальных гиперболических функций.
Таким же образом можно найти производные
остальных гиперболических функций.По формуле производной обратной функции
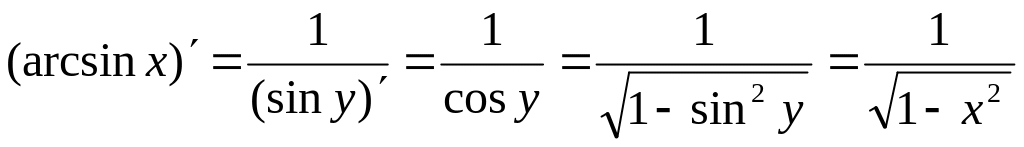 .
.
 .
.
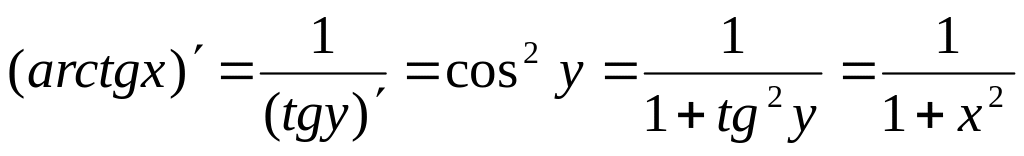 .
.
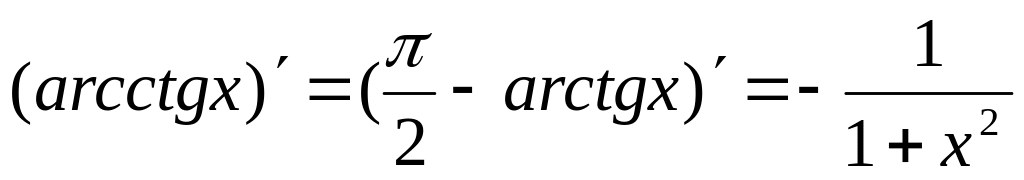 .
.Если
 – произвольное действительное число,
то
– произвольное действительное число,
то
![]() .
.
В результате получена таблица основных производных:
№ |
f(x) |
f΄(x) |
№ |
f(x) |
f΄(x) |
1 |
C |
0 |
9 |
ctgx |
|
2 |
xα |
αxα-1 |
10 |
shx |
chx |
3 |
ax |
axlna |
11 |
chx |
shx |
4 |
ex |
ex |
12 |
thx |
|
5 |
lnx |
|
13 |
cthx |
|
6 |
sinx |
cosx |
14 |
arcsinx |
|
7 |
cosx |
-sinx |
15 |
arccosx |
|
8 |
tgx |
|
16 |
arctgx |
|
|
|
|
17 |
arcctgx |
|
3.7 Метод логарифмическое дифференцирование. Производная показательно-степенной функции
Логарифмическим дифференцированием
называется вычисление производной от
логарифма функции
![]() .
.
![]() ,
,
Решение:
![]() ,
ОДЗ
,
ОДЗ
![]() .
.
![]() .
.
![]() .
.
Применение предварительного логарифмирования часто упрощает вычисление производной.
Пусть
![]() на некотором множестве значений аргумента
и дифференцируема на этом множестве.
Тогда по формуле производной сложной
функции
на некотором множестве значений аргумента
и дифференцируема на этом множестве.
Тогда по формуле производной сложной
функции
![]() откуда
откуда
![]() . (3.9)
. (3.9)
Эту формулу удобно использовать в тех случаях, когда производную натурального логарифма данной функции найти проще, чем производную самой функции.
![]()
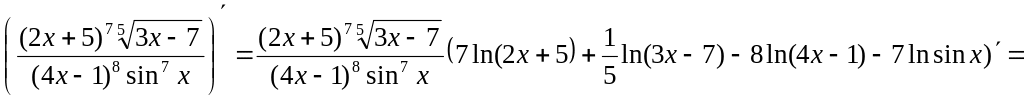
=![]()
Определения 3.5. Функция вида
![]() называется показательно степенной.
Ее производная должна вычисляться с
помощью логарифмического дифференцирования
(обратить внимание, что формулы для
показательной и степенной функций не
подходят!)
называется показательно степенной.
Ее производная должна вычисляться с
помощью логарифмического дифференцирования
(обратить внимание, что формулы для
показательной и степенной функций не
подходят!)
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
3.8 Дифференцирование функций, заданных неявно и параметрически
Если уравнение
![]() неявно задает функцию
,
то для того, чтобы найти производную от
этой функции
неявно задает функцию
,
то для того, чтобы найти производную от
этой функции
![]() необходимо продифференцировать правую
и левую часть тождества, помня, что
- независимая переменная, а
- неизвестная функция от
.
необходимо продифференцировать правую
и левую часть тождества, помня, что
- независимая переменная, а
- неизвестная функция от
.
Если функция
задана в виде:
![]() ,
причем функция
,
причем функция
![]() имеет обратную функцию
имеет обратную функцию
![]() ,
то
,
то
![]() ,
и
,
и
![]() . (3.10)
. (3.10)
Полученная формула дает возможность находить производную функции, заданной параметрически, без определения непосредственной зависимости у от х.
![]() ,
,
![]() – параметрические уравнения кривой,
называемой циклоидой. Найдем
:
– параметрические уравнения кривой,
называемой циклоидой. Найдем
:
![]() ,
,
![]() ,
,
![]() .
.
