
- •3 Дифференциальное исчисление 2
- •4 Применение производной 12
- •3 Дифференциальное исчисление
- •3.1 Производная функции, ее геометрический и механический смысл. Уравнение касательной к графику функции
- •3.2 Дифференцируемость функции. Дифференцируемость функции, ее связь с непрерывностью. Дифференциал функции, его геометрический смысл
- •3.3 Свойства производной (правила дифференцирования)
- •3.4 Производная сложной и обратной функций
- •3.5 Инвариантность формы дифференциала
- •3.6 Таблица производных
- •3.7 Метод логарифмическое дифференцирование. Производная показательно-степенной функции
- •3.8 Дифференцирование функций, заданных неявно и параметрически
- •3.9 Производные и дифференциалы высших порядков, их свойства
- •3.10 Точки экстремума функции. Теоремы Ферма и Ролля
- •3.11 Теоремы Лагранжа и Коши
- •4 Применение производной
- •4.1 Правило Лопиталя. Раскрытие неопределенностей.
- •4.2 Уравнение касательной к графику функции.
- •4.3 Формула Тейлора с остаточным членом в форме Пеано и в форме Лагранжа
- •4.4 Разложение основных элементарных функций по формуле Тейлора
- •4.5 Условия возрастания и убывания функции. Экстремумы функции, необходимое условие. Достаточные условия
- •4.6 Отыскание наибольшего и наименьшего значений функции, дифференцируемой на отрезке
- •4.7 Исследование выпуклости функции. Точки перегиба, их нахождение
- •4.8 Асимптоты функций
- •4.9 Общая схема исследования функции и построения ее графика
Содержание
3 Дифференциальное исчисление 2
3.1 Производная функции, ее геометрический и механический смысл. Уравнение касательной к графику функции 2
3.2 Дифференцируемость функции. Дифференцируемость функции, ее связь с непрерывностью. Дифференциал функции, его геометрический смысл 3
3.3 Свойства производной (правила дифференцирования) 4
3.4 Производная сложной и обратной функций 5
3.5 Инвариантность формы дифференциала 6
3.6 Таблица производных 6
3.7 Метод логарифмическое дифференцирование. Производная показательно-степенной функции 7
3.8 Дифференцирование функций, заданных неявно и параметрически 8
3.9 Производные и дифференциалы высших порядков, их свойства 8
3.10 Точки экстремума функции. Теоремы Ферма и Ролля 10
3.11 Теоремы Лагранжа и Коши 11
4 Применение производной 12
4.1 Правило Лопиталя. Раскрытие неопределенностей. 12
4.2 Уравнение касательной к графику функции. 14
4.3 Формула Тейлора с остаточным членом в форме Пеано и в форме Лагранжа 14
4.4 Разложение основных элементарных функций по формуле Тейлора 16
4.5 Условия возрастания и убывания функции. Экстремумы функции, необходимое условие. Достаточные условия 17
4.6 Отыскание наибольшего и наименьшего значений функции, дифференцируемой на отрезке 19
4.7 Исследование выпуклости функции. Точки перегиба, их нахождение 20
4.8 Асимптоты функций 22
4.9 Общая схема исследования функции и построения ее графика 23
3 Дифференциальное исчисление
Дифференциальное исчисление – часть математического анализа, изучающая свойства и применение производных и дифференциалов числовых функций.
3.1 Производная функции, ее геометрический и механический смысл. Уравнение касательной к графику функции
Рассмотрим функцию
![]() ,
заданную в окрестности точки х0.
,
заданную в окрестности точки х0.
Определение 3.1. Если
существует конечный предел
![]() ,
то он называется производной
функции
,
то он называется производной
функции
![]() в точке
в точке
![]() .
.
Обозначение:
![]() . (3.1)
. (3.1)
Разность
![]() называется приращением аргумента,
а
называется приращением аргумента,
а
![]() - приращением функции. Таким
образом, можно определить производную
как
- приращением функции. Таким
образом, можно определить производную
как
![]() .
.
С помощью определения производной найти
производную функции
![]()
Решение:
О.Д.З.
![]()
![]() О.Д.З.
О.Д.З.
![]()
![]()
![]()
![]() т.к. точка
т.к. точка
![]() -
любая точка из области определения
-
любая точка из области определения
![]() ,
то
,
то
![]()
Геометрический смысл производной.
Р
Рисунок 3.1 -
Геометрический смысл производной
функции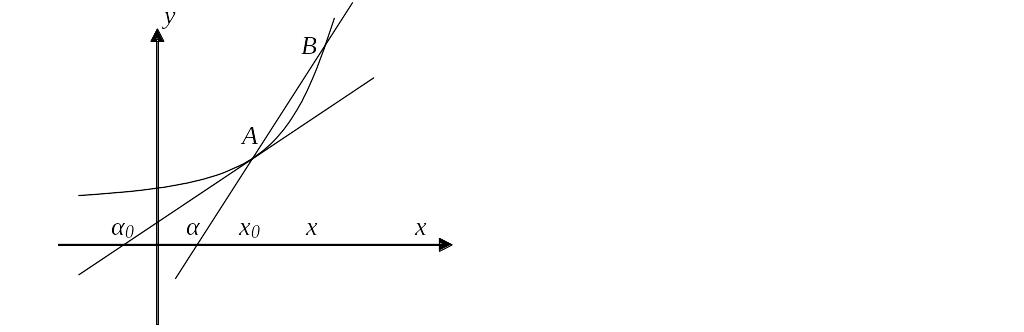
![]() .
Если обозначить разность ординат этих
точек
.
Если обозначить разность ординат этих
точек
![]() ,
то тангенс угла α, образованного секущей
с осью Ох, можно представить так:
,
то тангенс угла α, образованного секущей
с осью Ох, можно представить так:
![]() .
Если
.
Если
![]() ,
точка В перемещается по кривой, приближаясь
к точке А, и секущая при совпадении точек
В и А превращается в касательную к
графику функции, образующую с осью Ох
угол α0. При этом
,
точка В перемещается по кривой, приближаясь
к точке А, и секущая при совпадении точек
В и А превращается в касательную к
графику функции, образующую с осью Ох
угол α0. При этом
![]() Следовательно, значение производной
при данном значении
равно тангенсу угла, образованного
касательной к графику функции в точке
с соответствующим значением х с
положительным направлением оси Ох.
Следовательно, значение производной
при данном значении
равно тангенсу угла, образованного
касательной к графику функции в точке
с соответствующим значением х с
положительным направлением оси Ох.
Механический смысл производной.
Рассмотрим прямолинейное движение
тела, для которого пройденное расстояние
есть функция от времени:
![]() .
Среднюю скорость за время
.
Среднюю скорость за время
![]() можно определить по формуле:
можно определить по формуле:
![]() .
Для определения мгновенной скорости
тела в данный момент времени устремим
к нулю. Получим:
.
Для определения мгновенной скорости
тела в данный момент времени устремим
к нулю. Получим:
![]() Таким образом, производная от расстояния
в данный момент времени равна мгновенной
скорости движения в этот момент.
Соответственно производная любой
функции при данном значении аргумента
равна скорости изменения этой функции
при рассматриваемом
.
Таким образом, производная от расстояния
в данный момент времени равна мгновенной
скорости движения в этот момент.
Соответственно производная любой
функции при данном значении аргумента
равна скорости изменения этой функции
при рассматриваемом
.
Определение 3.2. Производной функции справа от точки или правой производной называется
![]() ,
,
Определение 3.3. Производной функции слева от точки , или левой производной
![]() .
.
Если производные функции слева и справа
от точки
![]() не равны, то производная в этой точке
не существует.
не равны, то производная в этой точке
не существует.
Найти левую и правую производную функции
![]() в точке
в точке
![]() .
Сделать вывод о существовании производной.
.
Сделать вывод о существовании производной.
Решение.
![]() .
.
![]() .
.
Производная этой функции в точке не существует.
