1.Мультипликативная производственная функция (Кобба-Дугласа).

Мультипликативная ПФ задается выражением

X = AK a1 * L a2,

a1 > 0,

a2 > 0

А – коэффициент нейтрального технического процесса

К – основные фонды

L – численность населения

При отсутствии одного из ресурсов производство невозможно.

Частным случаем этой функции служит функция Кобба-Дугласа

X =AK aL1a

где

a1 = a ,

a2 = 1 - a

Мультипликативная ПФ определяется по временному ряду выпусков и затрат ресурсов (

X, K, L), t=1,...,T

где T – длина временного ряда, при этом предполагается, что имеет место T соотношений.

2. Модель установления равновесной цены.

Равновесная (рыночная) цена устанавливается под воздействием спроса и предложения.

1. Цена на рынке стремится к такому уровню, при котором спрос равнее предложению.

2. Если под воздействием неценовых факторов произойдет изменение в спросе или предложении, то установится новая равновесная цена, соответствующая новому состоянию спроса и предложения

Равновесная цена (РЕ) - цена, уравновешивающая функцию спроса и функцию предложения, в результате действия конкурентных сил. QE=QD=QS.

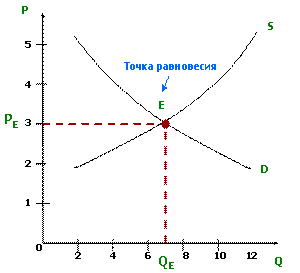
Где P – цена, Q – объем, D – спрос, S- предложение.

3.Геометрическое решение задачи линейного программирования. Анализ моделей на чувствительность. Экономико-математический анализ полученных оптимальных решений.

Основная задача линейного программирования (ОЗЛП) ставится следующим образом: Имеется ряд переменных . Требуется найти такие их неотрицательные значения, которые удовлетворяли бы системе линейных уравнений:

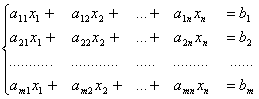
и, кроме того, обращали бы в минимум линейную целевую функцию (ЦФ)

Допустимым решением ОЗЛП называют любую совокупность переменных , удовлетворяющую уравнениям.

Оптимальным решением называют то из допустимых решений, при котором ЦФ обращается в минимум.

На практике ограничения в задаче линейного программирования часто заданы не уравнениями, а неравенствами. В этом случае можно перейти к основной задаче линейного программирования.

Таким образом, имеем общую задачу линейного программирования - найти неотрицательные , чтобы они удовлетворяли системе уравнений и обращали в минимум .

Для решения задач анализа чувствительности ограничения линейной модели классифицируются следующим образом. Связывающие ограничения проходят через оптимальную точку. Несвязывающие ограничения не проходят через оптимальную точку. Аналогично ресурс, представляемый связывающим ограничением, называют дефицитным, а ресурс, представляемый несвязывающим ограничением – недефицитным. Ограничение называют избыточным в том случае, если его исключение не влияет на ОДР и, следовательно, на оптимальное решение. Выделяют следующие три задачи анализа на чувствительность.

1. Анализ сокращения или увеличения ресурсов:

- на сколько можно увеличить (ограничения типа ) запас дефицитного ресурса для улучшения оптимального значения ЦФ?

-на сколько можно уменьшить (ограничения типа ) запас недефицитного ресурса при сохранении оптимального значения ЦФ?

2. Увеличение (ограничения типа ) запаса какого из ресурсов наиболее выгодно?

3. Анализ изменения коэффициентов ЦФ: каков диапазон изменения коэффициентов ЦФ, при котором не меняется оптимальное решение?