I

Механика / Кинематика поступательного и вращательного движения.

Механика / Динамика поступательного движения

Механика / Динамика вращательного движения

Механика / Работа. Энергия.

№1 Тело массы поднимают по наклонной плоскости. Высота наклонной плоскости , длина ее основания коэффициент трения . Минимальная работа, которую надо совершить, в джоулях равна …

Решение:

Минимальная сила, которую надо приложить к телу, чтобы поднимать его по наклонной плоскости без ускорения, равна сумме составляющей силы тяжести, параллельной наклонной плоскости, и силы трения: . Работа равна , где l – длина наклонной плоскости. Учитывая, что , получим . Следовательно, минимальная работа .

№2 Тело движется вдоль оси под действием силы, зависимость которой от координаты представлена на рисунке:

Р абота силы на пути определяется выражением …

Решение:

Работа переменной силы в случае одномерного движения на участке 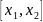определяется как интеграл: . На графике зависимости силы от координаты искомая работа представлена площадью, ограниченной кривой зависимости и осью координат (геометрический смысл интеграла). Следовательно, искомая работа численно равна площади трапеции ABCD, то есть произведению полусуммы оснований на высоту:

.

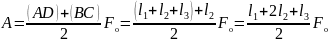№3

При увеличении давления в 3 раза и уменьшении объема в 2 раза внутренняя энергия идеального газа….

Решение.

Внутренняя энергия идеального газа равна (учитываем, что ), где давление, объем, полное число степеней свободы, универсальная газовая постоянная, абсолютная температура, масса газа, Учитывая, что , , получаем

. Следовательно,

Уменьшится в 6 раз

• Увеличится в 1,5 раза

Увеличится в 6 раз

Уменьшится в 1,5 раза

№4

На рисунке показан график зависимости потенциальной энергии от координаты х.

График зависимости проекции силы F(x)от координаты х имеет вид…

Решение:

Потенциальная энергия ,как видно из графика, пропорциональна квадрату координаты

-коэф-т пропорциональности. Проекция силы F(x)на ось Х связана с потенциальной энергией соотношением 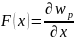и равна

График зависимости имеет вид

Механика / Законы сохранения в механике

Механика/ элементы специальной теории относительности

Средняя энергия молекул.

Тема: Распределения Максвелла и Больцмана

Первое начало термодинамики.

Второе Начало термодинамики. Энтропия

Законы постоянного тока.

Электростатическое поле в вакууме

Магнитостатика

Явление электромагнитной индукции.

Тема: Электрические и магнитные свойства вещества

Свободные вынужденные колебания.

№1 Колебание материальной точки, возникающее под действием внешней периодически изменяющейся силы, происходит по закону:

, где – коэффициент затухания; и циклические частоты соответственно собственных и вынужденных колебаний; амплитуда вынуждающей силы, отнесенная к массе тела. Зависимость смещения материальной точки от времени имеет вид, показаний на рисунке…

Решение.

Уравнение вынужденных колебаний - это линейное неоднородное дифференциальное уравнение, решение которого равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения . Общее решение играет существенную роль только в начальной стадии процесса установления гармонических колебаний с частотой вынужденных колебаний постепенно нарастает, и затем устанавливается гармоническое колебание с частотой вынуждающей силы:

№2

Шарик ,прикрепленный к пружине(пружинный маятник) и насажденный на горизонттальную направляющую,совершаетгармонические колебания.

На графике представлена зависимость проекции силы упругости пружины на положительное направление оси Х от координаты шарика.

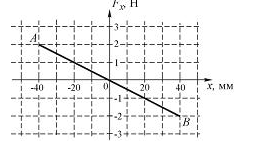
В положении В энергия пружинного маятника в мДж равна…

Решение:

В положении В пружинный маятник обладает потенциальной энергией, кинетическая энергия равна нулю.Потенциальную энергию можно найти по формуле П= - коэффициент жесткости пружины, х-растяжение(сжатие)пружины.Жесткость пружины можно определить,используя график: .Величину растяжения(сжатия)пружины в положении B также можно определить из графика:x=40

Сложение гармоничных колебаний

№1 Складываются два гармоничных колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз, равной …

Решение.

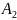Амплитуда результирующего колебания, полученного при сложении двух гармонических колебаний одного направления с одинаковыми частотами, определяется по формуле , где и - амплитуда складываемых колебаний; и - их начальные фазы. Следует заметить, если равны периоды колебаний, то равны и их частоты, так как . Амплитуда результирующего колебания будет максимальной, если , следовательно,

• 0

Уравнения Максвелла

№1

Уравнения Максвелла яв-ся основными законами классической макроскопическойэлектродинамики,сформулированными на основе обобщения важнейших законов электростатики и электромагнетзма.Эти уравнения в интегральной форме имеют вид:

1)

2)

3)

4)

Второе уравнение Максвелла яв-ся обобщением…

Решение:

Максвелл обобщил закон постоянного тока в среде ,предположив,что переменное электрическое поле,так же как и электрический ток,яв-ся источником магнитного поля.Максвеллввел в рассмотрение новую физичекую величину ,названную им током смещения,причем плотность тока смещения равна

Ответ:

Закона полного тока в среде.

Волны. Уравнение волны.

№1

Уравнение плоской синусоидальной волны, распространяется вдоль оси OX, имеет вид . При этом длина волны равна …

Решение.

В общем случае уравнение плоской синусоидальной волны, распространяющейся вдоль положительного направления оси OX в среде, не поглощающей энергию, имеет вид , здесь - амплитуда волны, - циклическая частота, начальная фаза волны, фаза плоской волны, волновое число, λ –длина волны. Из уравнения следует, что , а

№2

Плоская звуковая волнаἐ(х,t)=A cos( распространяется в упругой среде.Скорость колебания частиц среды,отстоящих от источника на расстоянии x= в момент времени t=T/4 равна…

Решение:

Скорость колебания частиц среды равна:𝞾= =-A ,где A-амплитуда волны; -циклическая частота волны;T-период колебаний;k=2 волновое число;𝛌-длина волны;( )-фаза волны.Скорость частиц среды,находящихся от источника на расстоянии x= 𝛌/6,в момент времени t=T/4 равна 𝞾=-A =-A =-A .Cледовательно , 𝞾=-A .

№3

Сейсмически упругая волна,падающая под углом 45 на границу раздела между двумя слоями земной коры с различными свойствами,испытывает преломление,причем угол преломления равен .Если в первой среде волна распространяется со скоростью 5,6 км/с,то во второй среде скорость( в км/с) сейсмической волны равна…

Решение:

Сейсмическая волна испытывает преломление,поскольку скорость распространения волны при переходе из одной среды в другую меняется. ,где -угол падения, -угол преломления, скорость распространения волны в первой среде, -скорость распространения волны во второй среде.

№4

Поперечными волнами являются…

Решение:

В данной задаче упругии поперечными волнами являются волны,распространяющиеся вдоль струн музыкальных инструментов ,т.к в струне возникает деформация сдвига,и частички струны колеблются в напрвлении,перпендикулярном направлению распространения волны вдоль струны.Радиоволны и световые волны-электромагнитные,следовательно,также поперечные.В электромагнитной волне векторы напряженностей электрического и магнитного полей колеблются в плоскостях ,перпендикулярных направлению распространения волны.

Ответ:радиоволны,световые волны в вакууме,волны,распространяющиеся вдоль струн музыкальных инструментов.

Энергия волны. Перенос энергии волной.

№1

В упругой среде плотности распространяется плоская синусоидальная волна. Если амплитуда волны увеличится в 4 раза, то плотность потока энергии (вектор Умова) увеличится в_____ раз(-а).

Решение.

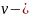Плотность потока энергии, то есть количество энергии, переносимой волны за единицу времени через единицу площади. Равно , где объемная плотность энергии, скорость переноса энергии волной (для синусоидальной волны эта скорость равна фазовой скорости). Среднее значение объемной плотности энергии равно , где амплитуда волны, частота. Следовательно, плотность потока энергии увеличится в 16 раз.

№2

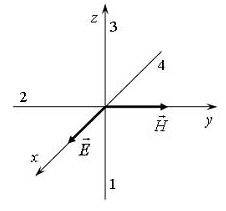
На рисунке показана ориентация векторов напряженности электрического и магнитного полей в электромагнитной волне.Вектор плотности потока энергии электромагнитного поля ориентирован в направлении….

Решение:

Плотность потока энергии электромагнитного поля- вектор,называемый вектором Умова-Пойтинга,-определяется в векторной форме как , где и – соответственно векторы напряженностей электрической и магнитной составляющих электромагнитной волны.Векторы , являются правой упорядоченной тройкой векторов.

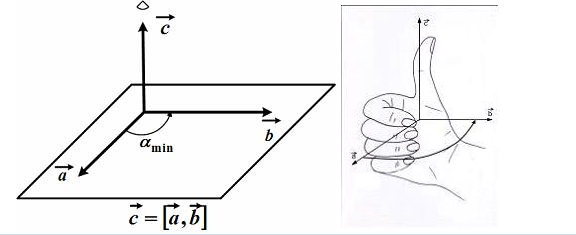
На рисунке показано,как найти направление результирующего вектора векторного произведения векторов .Для нашего случая

Вектор направлен вдоль оси Z, т.е ориентирован в направлении 3.

№3

Если в электромагнитной волне,распространяющейся в вакууме,значения напряженностей электрического и магнитного полей соответственно равны E=750 В/м, H=2 А/м, то объемная плотность энергии в микроджоулях на кубический метр составляет…

Решление:

Плотность потока энергии электромагнитной волны(вектор Умова-Пойнтинга)равна S=E H Также S= где - объемная плотность энергии, -скорость света.Следовательно,