6.5 Свойства функций алгебры логики

1. Функция штрих Шеффера { / }.

Свойства функции штрих Шеффера х₁ / х₂ = = ₁ + ₂

• х / х = ( т.к. х / х = = )

• х / 1 =

• х / 0 = 1

• / 1 = х

• / 0 = 1

• х / = 1

• Для функции штрих Шеффера справедливо свойство коммутативности для двух переменных, т.е. х₁ / х₂ = х₂ / х₁

Очередность операций для функции штрих Шеффера с n переменными устанавливается с помощью скобок.

Свойства ассоциативности и дистрибутивности для функции штрих Шеффера не справедливы.

2. Функция стрелка Пирса = ₁ + ₂ = х₁ ↓ х₂

• х ↓ х = (т.к. х ↓ х = = )

• х ↓ 0 =

• х ↓ 1 = 0

• х ↓ = 0

• ↓ 1 = 0

• ↓ 0 = х

• х₁ ↓ х₂ = х₂ ↓ х₁ свойство коммутативности выполняется только для двух переменных.

Для установления приоритетов выполнения операции стрелка Пирса, обязательно должны использоваться скобки.

Для функции стрелка Пирса свойства ассоциативности и дистрибутивности несправедливы.

3. Функция сложение по модулю 2 (х₁ х₂).

Через отрицание, конъюнкцию и дизъюнкцию функция сложения по модулю 2 выражается следующим образом:

х1	х2	х1 ⊕ х2	СДНФ
0	0	0
0	1	1	1 х2
1	0	1	х1 2
1	1	0

х₁ ⊕ х₂ = х_{1 2} + ₁ х₂;

Функция сложения по модулю 2 обладает следующими свойствами:

• коммутативности х₁ ⊕ х₂ = х₂ ⊕ х₁

• ассоциативности х₁ ⊕ (х₂ ⊕ х₁) = (х₁ ⊕ х₂) ⊕ х₃

• дистрибутивности х₁ (х₂ ⊕ х₃) = х₁ х₂ ⊕ х₁ х₃

Для этой функции справедливы аксиомы:

х ⊕ х = 0

х ⊕ 1 =

х ⊕ = 1

х ⊕ 0 = х

х₁ ⊕ х₂ = ₁ ⊕ ₂

х₁ ⊕ ₂ = х₁~ х₂

₁ ⊕ х₂ = х₁ ~ х₂

= х₁ ~ х₂

На основании аксиом и свойств можно вывести правила перевода функций отрицание, конъюнкция, дизъюнкция через функцию сложения по модулю 2 и наоборот.

₁ = х₁ ⊕ 1;

х₁ + х₂ = х₁ ⊕ х₂ ⊕ х₁ х₂

х₁ х₂ = (х₁ ⊕ х₂) ⊕ (х₁ + х₂)

4. Функция равнозначности (х₁ ~ х₂) выражается через отрицание, конъюнкцию и дизъюнкцию следующим образом:

х1	х2	х1 ~ х2	СДНФ
0	0	1	1 2
0	1	0
1	0	0
1	1	1	х1 х2

х₁ ~ х₂ = х₁ х₂ + _{1 2}

Свойства функции равнозначности:

• х ~ х = 1

• х ~ 0 =

• х ~ 1 = х

• х ~ = 0

• х₁ ~ х₂ = ₁ ~ ₂

• х₁ ~ ₂ = х₁ ⊕ х₂

• ₁ ~ х₂ = х₁ х₂

• = х₁ ⊕ х₂

• Для двух переменных выполняется свойство коммутативности

х₁ ~ х₂ = х₂ ~ х₁

Свойства ассоциативности и дистрибутивности для этой функции не выполняются.

Функция импликация (х₁ → х₂) выражается через отрицание и дизъюнкцию следующим образом:

х1	х2	х1 → х2	СКНФ
0	0	1
0	1	1
1	0	0	1 + х2
1	1	1

х₁ → х₂ = ₁ + х₂

Для функции импликации справедливы аксиомы:

х → х = 1

х → =

х → 1 = 1

0 → х = 1

х → 0 =

1 → =

х₁ → х₂ = ₂ → ₁

х₁ ∙ х₂ = ₂

х₁ + х₂ = ₁ → х₂ = ₂ → х₁

Свойства коммутативности, ассоциативности и дистрибутивности для этой функции не справедливы.

5. Функция коимпликация ( 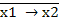) выражается через отрицание и конъюнкцию следующим образом:

= х_{1 2}

Для функции коимпликации справедливы аксиомы:

= 0

= х

= 0

=

= х

= 0

х₁ + х₂ =

х₁ х₂ =