1. Электрический заряд. Закон сохранения электрического заряда.

Э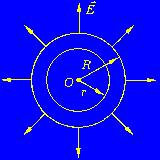 лектрический заря́д — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. Впервые электрический заряд был введён в законе Кулона в 1785 году.

Единица измерения заряда в СИ — кулон — электрический заряд, проходящий через поперечное сечение проводника при силе тока 1 А за время 1 с.

Различают два вида зарядов, условно называемых положительными и отрицательными; при этом одноименные заряженные частицы отталкиваются, а разноименные – притягиваются друг к другу.

Закон сохране́ния электри́ческого заря́да гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется.

2 Закон Кулона.

Зако́н Куло́на — это закон, описывающий силы взаимодействия между точечными электрическими зарядами.

Шарль Кулон дал такую формулировку закона:

Модуль силы взаимодействия двух точечных зарядов в вакууме прямо пропорционален произведению модулей этих зарядов и обратно пропорционален квадрату расстояния между ними

Иначе: Два точечных заряда в вакууме действуют друг на друга с силами, которые пропорциональны произведению модулей этих зарядов, обратно пропорциональны квадрату расстояния между ними и направлены вдоль прямой, соединяющей эти заряды. Эти силы называются электростатическими (кулоновскими).

Важно отметить, что для того, чтобы закон был верен, необходимы:

1) точечность зарядов — то есть расстояние между заряженными телами много больше их размеров — впрочем, можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии; 2)их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд; 3)взаимодействие в вакууме.

В векторном виде в формулировке Ш. Кулона закон записывается следующим образом:

3 Электростатическое поле. Напряженность поля. Принцип суперпозиции полей.

Электрическое поле — одна из составляющих электромагнитного поля; особый вид материи, существующий вокруг тел или частиц, обладающих электрическим зарядом, а также возникающий при изменении магнитного поля (например, в электромагнитных волнах). Электрическое поле непосредственно невидимо, но может быть обнаружено благодаря его силовому воздействию на заряженные тела.

Н апряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на неподвижный пробный заряд, помещенный в данную точку поля, к величине этого заряда q:

Принцип суперпозиции электрических полей. Напряженность электрического поля, одновременно создаваемого в некоторой точке пространства несколькими зарядами, равна сумме векторов напряженностей электрических полей, которые создавались бы в этой же точке каждым из зарядов по отдельности:

4 Электрический диполь.

С овокупность двух равных по величине разноименных точечных зарядов q, расположенных на некотором расстоянии друг от друга, малом по сравнению с расстоянием до рассматриваемой точки поля называется электрическим диполем.(рис.13.1) Произведение называется моментом диполя. Прямая линия, соединяющая заряды называется осью диполя. Обычно момент диполя считается направленным по оси диполя в сторону положительного заряда.

5 Теорема Остроградского-Гаусса для электростатического поля в вакууме.

Поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на ε₀. (1) В общем случае электрические заряды могут быть распределены с некоторой объемной плотностью ρ=dQ/dV, которая различна в разных местах пространства. Тогда суммарный заряд, заключенный внутри замкнутой поверхности S, которая охватывает некоторый объем V, (2). Используя формулу (2), теорему Гаусса (1) можно записать так: