13.Закон полного тока для тороидальной катушки. Понятие магнитного потока, потокосцепление.

Закон полного тока. Циркуляция вектора напряженности магнитного поля по замкнутому контуру равна полному току, пронизывающему этот контур:

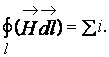
На ферромагнитном сердечнике тороидальной формы с площадью сечения  S и длиной средней линии  l располагается обмотка с числом витков  w и током  I (рис. 1.6).

Магнитный поток в сердечнике распределен равномерно, так что

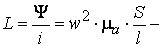
где		индуктивность катушки  [Гн].
Энергия, запасенная в катушке [Дж],

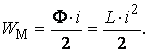
Понятие магнитного потока.

Рассмотрим сначала плоскую площадку S (рис. 5.10.1), находящуюся в однородном магнитном поле с индукцией В.

 

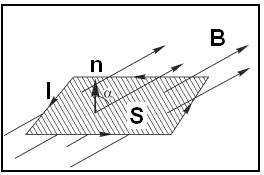Рис. 5.10.1

 Магнитным потоком или потоком вектора магнитной индукции сквозь площадку S называют величину

 

,

 

где Ф – магнитный поток, Вб;

В – магнитная индукция, Тл;

S – плоская площадка, м²;

α – угол между направлением нормали n к площадке и направлением индукции В;

Bn – проекция вектора В на нормаль n.

Если магнитное поле неоднородно и рассматриваемая поверхность не плоская, то ее можно разбить на бесконечно малые элементы dS. В этом случаи полный магнитный поток через всю поверхность будет равен

 

.

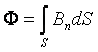Магнитный поток сквозь любую замкнутую поверхность равен нулю:

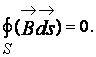
Общий магнитный поток, сцепляющийся со всеми витками катушки, называется потокосцеплением и численно равен сумме потоков, сцепляющихся с отдельными витками.

Часто реальное распределение потокосцепления по виткам катушки неизвестно, но его можно принять равномерным и одинаковым для всех витков, если реальную катушку заменить эквивалентной с другим числом витков w_э, сохраняя при этом величину потокосцепления Y = w_эФ_m, где Ф_m - поток, сцепляющийся с внутренними витками катушки, а w_э - эквивалентное или эффективное число витков катушки.

Или проще говоря

Потокосцепление катушки  [Вб] равно произведению числа витков  w на пронизывающий их поток  F:

Можно также произвести замену реальной катушки на эквивалентную с сохранением числа витков  = wФ_n. Тогда для сохранения потокосцепления необходимо принять, что со всеми витками катушки сцепляется магнитный поток Ф_n=  /w .

14. Схема замещения катушки с магнитопроводом

Рассмотрим процессы в катушке с замкнутым ферромагнитным магнитопроводом, обмотка которой имеет  витков. Протекающий по обмотке ток  (рис. 6.8 а) создает магнитный поток. Основная часть этого потока  – замыкается по магнитопроводу, а меньшая часть – поток рассеяния , рассеивается в пространство. Обычно  составляет несколько процентов от . Если магнитопровод насыщен или имеет большой воздушный зазор, то поток  соизмерим с .

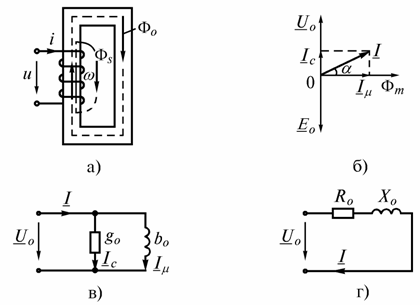
Рис. 6.8

 Если пренебречь активной составляющей сопротивления катушки и потоком рассеяния, то при питании катушки от источника синусоидального тока в ней будет возникать основной магнитный поток

. (6.4)

 Вследствие этого в витках катушки возникает ЭДС самоиндукции

. (6.5)

 Так как эта ЭДС равна напряжению источника, то

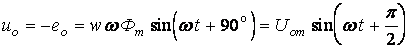. (6.6)

 Формулы (6.4) и (6.6) показывают, что вектор  опережает вектор  на 90°.

 Действующее значение этого напряжения

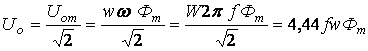. (6.7)

 Построим векторную диаграмму идеальной катушки ( = 0,  = 0). За исходный вектор примем вектор максимального значения магнитного потока  (рис. 6.8 б). Вектор напряжения  опережает вектор магнитного потока на 90°, а вектор ЭДС самоиндукции  равен вектору напряжения , но противоположен по направлению. Вектор действующего значения тока через катушку  опережает вектор  на угол , обусловленный гистерезисом. Представим вектор суммой двух составляющих: активной – проекцией вектора тока на вектор напряжения  и реактивной , которую принято называть током намагничивания. Тогда

. (6.8)

 Этому уравнению соответствует схема замещения (рис. 6.8 в), где ток   обусловлен потерями в магнитопроводе:

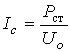. (6.9)

 Составляющая – это ток через идеализированную катушку (катушка, в магнитопроводе которой нет потерь энергии).

 Схему на рис. 6.8 в можно преобразовать в другую схему (рис. 6.8 г), используя проводимости ветвей

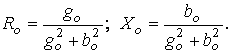
 В схемах (рис. 6.8 в и г)  – соответственно активная составляющая сопротивления и активная составляющая проводимости, учитывающие потери мощности в магнитопроводе;  – реактивная составляющая сопротивления и реактивная составляющая проводимости, обусловленные основным магнитным потоком.

 В схеме замещения реальной катушки учитываем активное сопротивление катушки  и реактивное сопротивление , обусловленное магнитным потоком рассеяния (рис. 6.9 а, б). В этих схемах участок ab называют ветвью намагничивания.

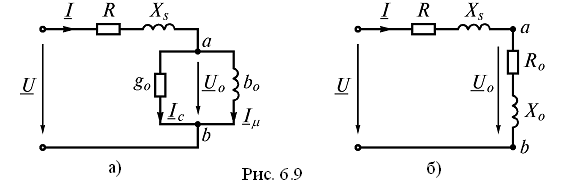
 Запишем уравнение по второму закону Кирхгофа для схем (рис. 6.9) в комплексной форме

. (6.10)

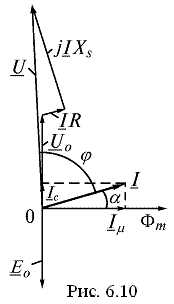
 Применим это уравнение для построения векторной диаграммы реальной катушки (рис. 6.10). Угол, обусловленный гистерезисом

.

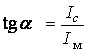
 Практически  или .

 Коэффициент мощности

. (6.11)

 Активная мощность катушки с ферромагнитным магнитопроводом состоит из потерь мощности в проводах  и потерь мощности в магнитопроводе

  . (6.12)

 Чем больше угол , тем больше активная составляющая тока  и потери в магнитопроводе. Поэтому угол  называют углом потерь в магнитопроводе.

Действующим называют значение переменного тока, эквивалентное постоянному току по тепловому действию, т. е. действующее значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, выделит в определенном сопротивлении такое же количество тепла, что и переменный ток.

Действующие значения переменных величин обозначаются прописными (заглавными) буквами без индексов: I, U, Е. Действующие значения синусоидальных величин меньше амплитудных значений этих величин в  раза, т. е.

; ; (4.12)

Так как действующие значения синусоидальных величин пропорциональны их амплитудным значениям, то в дальнейшем, длина вектора на векторной диаграмме будет соответствовать действующему значению синусоидальной величины.

Номинальные величины тока, напряжения и ЭДС источников и потребителей переменного тока являются действующими значениями этих величин.

Амперметры и вольтметры переменного тока измеряют преимущественно действующие значения тока и напряжения.

Отклонение переменной величины от синусоиды характеризует коэффициент формы и коэффициент амплитуды . Для синусоиды Кф =1,11; Ка =1,41.