
- •1) Понятие матрицы,операции.
- •1. Сложение матриц - поэлементная операция
- •2. Вычитание матриц - поэлементная операция
- •3. Произведение матрицы на число - поэлементная операция
- •5)Решение матричных уравнений
- •11) Вещественное Евклидово пр-во.И св-ва
- •15) Ортогональный и нормир бизис
- •19) Метод лагранжа
- •22)Диф.Ур.1го поряд.С раздел перем
- •25) Уравнение Бернулли
15) Ортогональный и нормир бизис
Нормированный
базис
Система
векторов ![]() для
которой
для
которой
![]()
называется ортонормированной.
Во
всяком пространстве ![]() существует
ортонормированный базис. Из произвольного
базиса
существует
ортонормированный базис. Из произвольного
базиса ![]() пространства
пространства ![]() ортогональный
базис может быть построен с помощью
процесса ортогонализации:
ортогональный
базис может быть построен с помощью
процесса ортогонализации:
![]()
![]() где
где ![]()
![]() где
где ![]()
![]() где
где ![]()
Пронормировав
каждый вектор ![]() получим
ортонормированный базис. В ортонормированном
базисе (
получим
ортонормированный базис. В ортонормированном
базисе (![]() )
для векторов
)
для векторов ![]()
![]() имеем:
имеем:
![]()
18) П-ие о квадратич. Форме.
Определение 1. Скалярная функция векторного аргумента, которая представляет собой однородный многочлен второго порядка, называется квадратичной формой.
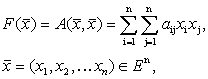
![]() R.
R.
Определение
2. Матрица,
составленная из коэффициентов
квадратичной формы ![]() ,
называется матрицей квадратичной
формы.
,
называется матрицей квадратичной
формы.
Пример. ![]() R,
R, ![]() .
.
![]() ,
,
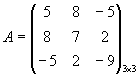 .
.
Матрица квадратичной формы симметрична относительно главной диагонали.
Теорема 1. Любая симметричная квадратная матрица порядка n имеет n действительных собственных значений и собственных векторов. Собственные векторы симметричной матрицы попарно ортогональны.
Следовательно,
собственные векторы матрицы образуют базис
в пространстве ![]() .
.
Определение 3. Рангом квадратичной формы называется ранг матрицы А.
Определение
4. Квадратичная
форма ![]() называется
положительно определенной (отрицательно
определенной), если для любого
называется
положительно определенной (отрицательно
определенной), если для любого ![]()
>0 (<0).
Теорема 2 (критерий Сильвестра). Квадратичная форма является положительно определенной тогда и только тогда, когда все левые верхние угловые миноры матрицы А являются положительными, т.е.
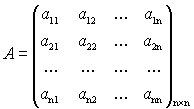 ,
,
![]() ,
,
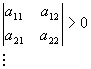 ,
,
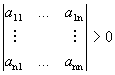
19) Метод лагранжа
Метод Лагранжа — метод приведения квадратичной формы к каноническому виду, указанный в 1759 году Лагранжем.
[править]Описание
Данный метод состоит в последовательном выделении в квадратичной форме полных квадратов. Пусть
![]()
есть данная квадратичная форма. Возможны два случая:
хотя бы один из коэффициентов
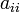 при
квадратах отличен от нуля. Не нарушая
общности, будем считать
при
квадратах отличен от нуля. Не нарушая
общности, будем считать 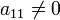 (этого
всегда можно добиться соответствующей
перенумерацией переменных);
(этого
всегда можно добиться соответствующей
перенумерацией переменных);все коэффициенты
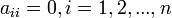 ,
но есть коэффициент
,
но есть коэффициент  ,
отличный от нуля (для определённости
пусть будет
,
отличный от нуля (для определённости
пусть будет  ).
).
В первом случае преобразуем квадратичную форму следующим образом:
![]()
![]()
![]() ,
где
,
где
![]() ,
а через
,
а через ![]() обозначены
все остальные слагаемые.
обозначены
все остальные слагаемые.
![]() представляет
собой квадратичную форму от n-1
переменных
представляет
собой квадратичную форму от n-1
переменных ![]() .
.
С ней поступают аналогичным образом и так далее.
Заметим,
что ![]()
Второй
случай заменой переменных ![]()
сводится к первому.
20) пр-еи к канонич виду. Преобразов. Базиса
Теорема
11.9. Если существует ортогональное
преобразование с матрицей С, приводящее
действительную квадратичную форму![]() К
каноническому виду
К
каноническому виду
![]()
(11.11)
То![]() -
характеристические числа матрицы
-
характеристические числа матрицы![]() Квадратичной
формы
Квадратичной
формы![]()
Теорема 11.10. Для любой действительной квадратичной формы существует ортогональное преобразование, приводящее ее к каноническому виду.
Теорема
11.11. Для любой, действительной
симметрической матрицы![]() Существует
такая ортогональная матрица
Существует
такая ортогональная матрица![]() Что
Что![]() -
диагональная матрица.
-
диагональная матрица.
Следствие. Любая действительная симметрическая матрица может быть приведена к диагональному виду.
Теорема 11.12. Если линейное преобразование действительного линейного пространства имеет действительную симметрическую матрицу в некотором ортонормированном базисе, то существует ортонормированный базис, состоящий из собственных векторов этого преобразования.
Из этих теорем следует правило нахождения ортогонального преобразования, приводящего квадратичную форму п переменных к каноническому вицу. Эго правило состоит в следующем: 1) записать матрицу данной квадратичной формы, найти ее собственные значения и п попарно ортогональных собственных векторов, пронормировать их; 2) составить матрицу из ортонормированных собственных вектор-сголбцов; 3) записать искомое ортогональное преобразование с помощью последней матрицы.
Пример
11.3. Найти ортогональное преобразование,
приводящее к каноническому виду
квадратичную форму двух переменных хи
х,,
![]()
Характеристическое уравнение (5-А.)(7-А,)-24 = 0, или А1 -12А.+ +11 = 0, имеет корни X, =1, А., =11, которые янляются собственными значениями матрицы А.
Найдем собственные векторы, соответствующие полученным собственным значениям. Координаты (л, I) этих векторов определяются из системы уравнений (10.12), которая в данном случае имеет вид
(5-А)« + 2>/бг = 0,0 гЛв + (7-А) 1 = 0.
При А, = 1, А, = 11 имеем две системы
4л + 2>/бг = 0, - 65 + 2->[б1 = 0,
2^б5+6/ = 0, 2^6в-А1 = 0.
Из этих систем находим собственные векторы и = (- (л/б/2) I, I), V = ((-Уб/з) I, I),
Где 1Ф 0. Положив 1х=—2, 1г =3, получим м= (Л,-2), V = (Л, 3).' Нормировав эти векторы, запишем их координаты в столбцы, составим матрицу В:
![]()
![]()
Дх,,х2) = 5х{ + 4-/бх, х2 + 1х[. .
![]()
Поскольку в данном случае я,, = 5, аи = аг{ = 2^6, а21 = 7, то матрица А этой квадратичной формы и ее характеристическое уравнение йе1(/4- ХЕ) = О запишутся так:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() С
помощью матрицы
С
помощью матрицы![]() Записываем
искомое ортогональное преобразование
Записываем
искомое ортогональное преобразование
Или
![]()
![]()
Это преобразование приводит данную квадратичную форму к каноническому виду
![]()
21)понятие о диф. Ур-ии
Определение 1. Уравнение, содержащее независимую переменную, функцию от этой независимой переменной и ее производные различных порядков, называется дифференциальным уравнением.
Определение 2. Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком дифференциального уравнения.
Дифференциальное уравнение n-го порядка имеет вид
F(x,y,y',y'', …, y(n))=0.
Определение 3. Дифференциальное уравнение n-го порядка называется линейным, если неизвестная функция и все ее производные входят в него в первой степени. Общий вид линейного дифференциального уравнения n-го порядка:
a0(x)y(n) + a1(x)y(n-1) + ... + an-1(x)y(1) + an(x)y = f(x). (1)
Определение 4. Линейное дифференциальное уравнение (1) называется однородным, если f(x) º 0, и неоднородным - в противном случае.
Примеры дифференциальных уравнений:
y'' - sin x y' + (cos x) y = tg x - линейное,
sin y' - cos y = ctg x - нелинейное,
y''' - y' = 0 - линейное,
(yIV)2 - 3y''' + y = 1 - нелинейное.
Определение 5. Решением дифференциального уравнения называется любая функция y = j(x), при подстановке которой в уравнение будет получено тождество. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения, график решения называют интегральной кривой.
Пример 1. y' - f(x) = 0 , Пример 2. y'' = 0,
y' = f(x), y' = C,
y = ò f(x)dx + C. y = C1x + C2.
Определение 6. Решение дифференциального уравнения n-го порядка, содержащее n произвольных постоянных, называется общим решением дифференциального уравнения.
Определение 7. Если в результате интегрирования дифференциального уравнения получена зависимость между y и x, из которой не удается явно выразить y через x (т.е. неизвестная функция задана неявно), то данную зависимость называют общим интегралом дифференциального уравнения.
Определение 8. Решение, полученное из общего при конкретных значениях произвольных постоянных, называется частным решением.
Пример. y'' + y = 0.
y = C1 cos x + C2 sin x - общее решение.
у1 = 3 cos x -2 sin x - частное решение.
Зада́ча Коши́ — одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла)дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).
Задача
Коши обычно возникает при анализе
процессов, определяемых дифференциальным
законом эволюции и начальным состоянием
(математическим выражением которых и
являются уравнение и начальное условие).
Этим мотивируется терминология и выбор
обозначений: начальные данные задаются
при ![]() ,
а решение отыскивается при
,
а решение отыскивается при ![]() .
.
От краевых задач задача Коши отличается тем, что область, в которой должно быть определено искомое решение, здесь заранее не указывается. Тем не менее, задачу Коши можно рассматривать как одну из краевых задач.
Основные вопросы, которые связаны с задачей Коши, таковы:
Существует ли (хотя бы локально) решение задачи Коши?
Если решение существует, то какова область его существования?
Является ли решение единственным?
Если решение единственно, то будет ли оно корректным, то есть непрерывным (в каком-либо смысле) относительно начальных данных?
Говорят,
что задача Коши имеет единственное
решение, если она имеет решение ![]() и
никакое другое решение не
отвечает интегральной
кривой,
которая в сколь угодно малой выколотой
окрестности точки
и
никакое другое решение не
отвечает интегральной
кривой,
которая в сколь угодно малой выколотой
окрестности точки ![]() имеет поле
направлений,
совпадающее с полем направлений
.
Точка
задаёт
начальные условия.
имеет поле
направлений,
совпадающее с полем направлений
.
Точка
задаёт
начальные условия.
21) Дифференциальные уравнения с разделяющимися переменными
Дифференциальное уравнение вида
![]()
или
![]()
называется дифференциальным уравнением с разделяющимися переменными.
Заметим, что в данных дифференциальных уравнениях каждая из функций зависит только от одной переменной, т.е. происходит разделение переменных.
Для
решения такого дифференциального
уравнения необходимо
домножить или разделить обе
части дифференциального
уравнения на
такое выражение, чтобы в одну часть
уравнения входили только функции
от ![]() и
и ![]() ,
в другую часть уравнения - только функции
от
,
в другую часть уравнения - только функции
от ![]() ,
, ![]() .
Затем в полученном дифференциальном
уравнении надо
проинтегрировать обе части:
.
Затем в полученном дифференциальном
уравнении надо
проинтегрировать обе части:
![]()
Следует заметить, что при делении обеих частей дифференциального уравнения на выражение, содержащее неизвестные и , могут быть потеряны решения, обращающие это выражение в ноль.
Обратим внимание, что дифференциальные уравнения с разделяющимися переменными легко сводятся к интегрированию. В общем случае получаем получаем дванеопределенных интеграла.
Пример 1 - решить дифференциальное уравнение
Заметим, что в дифференциальном уравнении можно разделить переменные, т.е. получаем,дифференциальное уравнение с разделяющимися переменными:
Пример 2 - решить дифференциальное уравнение
Заметим, что в дифференциальном уравнении можно разделить переменные, т.е. получаем,дифференциальное уравнение с разделяющимися переменными:
Пример 3 - решить дифференциальное уравнение
Заметим, что в дифференциальном уравнении можно разделить переменные, т.е. получаем,дифференциальное уравнение с разделяющимися переменными:
22) однород диф. Ур-е
Однородные дифференциальные уравнения
Однородное дифференциальное уравнение может быть записано в виде
![]()
или
![]()
где ![]() ,
, ![]() - однородные
функции одной и той же степени,
т.е. для некоторого натурального
числа
- однородные
функции одной и той же степени,
т.е. для некоторого натурального
числа ![]() и
для произвольного
и
для произвольного ![]() справедливы
равенства
справедливы
равенства
![]()
Для решения
однородного дифференциального
уравнения необходимо
сделать замену переменных ![]() ,
которая сводит однородное
дифференциальное уравнение кдифференциальному
уравнению с разделяющимися переменными.
,
которая сводит однородное
дифференциальное уравнение кдифференциальному
уравнению с разделяющимися переменными.
Пример 1 - решить дифференциальное уравнение
![]()
