1) Понятие матрицы,операции.
Матрицей размера m на n (записывается так m x n )называется совокупность mn комплексных чисел или элементов другого вида (многочлены, функции и т.д.), записанных в виде прямоугольной таблицы, которая состоит из m строк и n столбцов и взятая в круглые или прямоугольные или в двойные прямые скобки. При этом сами числа называются элементами матрицы и каждому элементу ставится в соответствие два числа -номер строки и номер столбца.
Элементы матрицыобозначают строчными латинскими буквами, снабженными двумя ai,j индексами: - элемент матрицы, расположенный в i-й строке и j-м столбце или коротко элемент в позиции (i,j). В общем виде матрица размера m на n может быть записана следующим образом
Действия над матрицами.
1. Сложение матриц - поэлементная операция
2. Вычитание матриц - поэлементная операция
3. Произведение матрицы на число - поэлементная операция
4. Умножение A*B матриц по правилу строка на столбец (число столбцов матрицы А должно быть равно числу строк матрицы B)Amk*Bkn=Cmn причем каждый элемент сij матрицы Cmn равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы B.
2)Определителем называется число, записанное в виде квадратной таблицы:
.
Определитель II порядка вычисляется по формуле:
Определитель n-го порядка вычисляется методом разложения по столбцу или строке.
СВОЙСТВО 1. Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, то есть
.
СВОЙСТВО 2. Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1. Например,
.
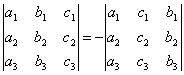СВОЙСТВО 3. Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.
СВОЙСТВО 4. Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k. Например,
.
СВОЙСТВО 5. Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случае предыдущего (при k=0).
СВОЙСТВО 6. Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю.
СВОЙСТВО 7. Если каждый элемент n-го столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце или соответственно в n-й строке имеет первые из упомянутых слагаемых, а другой - вторые; элементы, стоящие на остальных местах, у вех трех определителей одни и те же. Например,
СВОЙСТВО 8. Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится. Например,
.
3) Понятие определителя n-ого порядка.
Определителем квадратной матрицы n-ого порядка называется число, равное алгебраической сумме n членов, каждый из которых является произведением n-элементов матрицы, взятых по одному из каждой строки или столбца (причём знак каждого члена определяется как (-1)r(j), где r(j)-число инверсий). Теорема Лапласа: определитель квадратной матрицы равен сумме произведений элементов к.-л. строки или столбца на их алгебраические дополнения.
А) Метод Гаусса. Приведение к треугольному виду
Б) метод понижения порядка путем элементарных упрощений. Сделать все элементы столбца(строки) равными нулю, кроме одного, затем разложить определитель по этому столбцу(строке) и получить определитель меньшего порядка.
4) Пусть Аnxn квадратная матрица размера n на n. Обратной к матрице А называется матрица, обозначается А-1, (А в минус первой степени ), такая что
А×А-1 = А-1×А=Е.
Свойства:
а) (A-1)-1 = A;
б) (AB)-1 = B-1A-1
в) (AT)-1 = (A-1)-T.