1. Вероятностные характеристики измерительных сигналов

Математическая модель процесса передачи измерительной информации представляет собой модель случайного процесса с плотностью вероятности . Полезные сигналы и сигналы помех, действующие на информационно- измерительную системы, являются случайными процессами, которые могут быть характеризованы статистическими средними значениями и характеристиками.

Случайный процесс является более сложным случайным явлением, чем случайная величина, но его определение можно дать через случайную величину. Функция (рис.4) называется случайным процессом, если ее мгновенные значения являются случайными величинами [36]. Также как и случайная величина не может характеризоваться отдельным значением, так и случайный процесс нельзя определить какой-то одной, пусть и сложной функцией. Случайный процесс представляет собой множество реализаций (функций времени) . Реализация x­_i­(t) – фрагмент случайного процесса X(t), зафиксированный в результате i-го эксперимента ограниченной длительности T, следовательно, под реализацией понимают один из возможных исходов случайного процесса. Случайная величина ­­­­, соответствующая i-й реализации и j-му моменту времени, является мгновенным (выборочным) значением - частным случаем случайного процесса, а вероятностные характеристики случайного процесса основаны на характеристиках случайных величин, входящих в этот процесс. Совокупность мгновенных значений, соответствующих значениям различных реализаций в один и тот же момент времени t­_j­ , называется j-ой последовательностью процесса X(t). При решении прикладных задач чаще обращаются к реализациям, чем к последовательностям.

Экспериментально ансамбль реализаций случайного процесса может быть получен в результате одновременной регистрации выходных параметров x­_i­(t) на выходах однотипных объектов, например, измерительных приборов , в течение фиксированного интервала времени.

Если аргумент t изменяется непрерывно, зависимость X(t) представляет непрерывный случайный процесс (например, изменение погрешности измерительного прибора в течение длительного времени его работы) , если аргумент t является дискретной величиной – случайную последовательность или временной ряд (массив результатов измерения погрешности в известные моменты времени). Процесс X(t) , принимающий счетное ограниченное количество значений, называется дискретным случайным процессом (например, последовательность состояний работы оборудования информационно- измерительных систем или информационно- вычислительных комплексов) [37].

Определяя случайный процесс случайными величинами, находят вероятностные характеристики процессов, исходя из вероятностных характеристик этих величин.

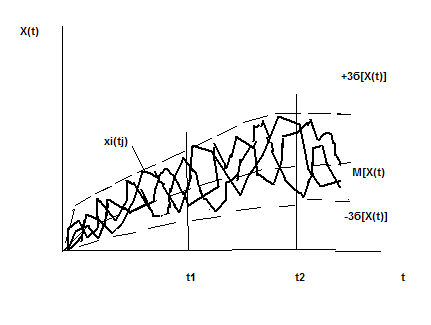
Рис.4. Графическое изображение случайного процесса

Наиболее полно описывают случайный процесс интегральная функция распределения вероятности

и дифференциальная функция распределения вероятности

.

­­В функциях распределения вероятности случайных процессов, в отличие от многомерных функций распределения вероятности случайных величин к аргументам x­_{i ­} добавляются переменные t­_j, показывающие, в какие моменты времени сняты отсчеты.

Для приближенного описания случайных процессов, также как и для описания случайных величин используют такие числовые характеристики, как математическое ожидание, дисперсия и т.д. Причем, эти числовые характеристики также являются функциями времени.

Наиболее часто используемыми вероятностными характеристиками являются.

1.Математическое ожидание ,

оценкой математического ожидания случайной функции является ее среднее значение .

2. Дисперсия – неслучайная функция

,

где - центрированный случайный процесс; значения дисперсии при каждом t­_j­ равны дисперсии случайной величины x_i(t­_j­).

Дисперсия случайной функции может быть найдена через дифференциальную функцию распределения вероятности случайной функции

;

Оценкой дисперсии является ее эмпирическое значение

.

Случайные процессы с одинаковыми математическими ожиданиями и дисперсиями могут существенно отличаться формой (рис.4).

3. Автокорреляционная функция характеризует статистическую связь между мгновенными значениями случайного процесса в различные моменты времени. Чем меньше значение автокорреляционной функции, тем в меньшей степени зависит значение измерительного сигнала в момент t­₁ от значения в момент t­_2.­. Определяется одним из следующих соотношений [38]

,

где t­_1­,t­_2­ –фиксированные моменты времени, в которых определены сечения случайной функции.

Так как при t­_1­=t­_2­­ , для одних и тех же сечений корреляционная функция обращается в дисперсию случайной функции.

Для каждой пары моментов времени автокорреляционная функция равна корреляционному моменту, статистическая оценка которого

,

В формулах, определяющих эмпирические оценки дисперсии и корреляционной функции, количество реализаций n уменьшается на единицу для получения несмещенной оценки;

4. Взаимно корреляционная функция определяет статистическую связь двух сигналов X(t) и Y(t+τ)

,

или

Изучение свойств случайных процессов с использованием корреляционных функций называют корреляционной теорией случайных процессов.

5. Спектральная плотность - неслучайная функция, устанавливающая плотность распределения его дисперсии по частоте ω, равна преобразованию Фурье соответствующей корреляционной функции

.

Корреляционная функция может быть выражена через спектральную плотность соотношением типа обратного преобразования Фурье .

Соотношения, позволяющие проводить преобразования спектральной плотности в корреляционную функцию и наоборот, носят название теоремы Хинчина- Винера.