1.2. Неоднозначность образов действительности

Физические измерения не обеспечивают условий отображения, описываемых чисто математически в предыдущем параграфе. Свойства анализаторов человека и средств измерения не позволяют установить точное равенство двух значений исследуемой характеристики объекта. Создавая образы действительности с помощью измерений, получают неоднозначные отображения: состояние а измеряемой характеристики отображается в множество значений области абстракции .

Элементы множества

, поставленные в соответствие состоянию а, неравнозначны.

Поэтому выбор элементов множества , в большей степени соотв. состоянию а, определяется мерой .

Если значения величин b дискретны, то

Если значения величин b носят непрерывный характер, то

Соответствие состояний измеряемых характеристик результатам измерения определяется как , при этом множества и { равномощны.

Графическое изображение этого соответствия приведено на рис.19. Состоянию а с вероятностью p=1 относится множество событий . Для определения измерительной шкалы из множества надо выбрать только один элемент .

Достоверность отображения состояний а характеристики Q в область абстракции также подразумевает, что функция отображения и обратного отображения должны быть определены не только для состояния а и значения , но и для близлежащих значений

где u – отклонение состояния а ; v – отклонение в области абстракции.

При использовании функции обратного отображения образом состояния а является множество , что означает, что существует несколько состояний которые интерпретируются как состояния а. Возникающий при этом интервал неопределенности обуславливается ограниченной способностью различения анализаторами человека или метрологических средств отдельных состояний измеряемой характеристики.

1.3. Решающие правила отображений

Однозначное отображение состояний измеряемых характеристик в область абстракции означает эквивалентность состояний величин. Создаваемый при этом образ действительности недостаточен, так как он не отражает те количественные отношения, в которых находятся образы состояний данной характеристики. Для достоверности отображения необходимо, чтобы отношения между состояниями а измеряемых характеристик были такими же, как и между значениями величин в области абстракции. Рассмотрим те отношения между значениями величин, которые имеют принципиальное значение, имея в виду что они аналогичны соотношениям между состояниями характеристик реальной области, т.е. изоморфны.

- Отношение эквивалентности состоит в том, что любые два элемента множества значений величин состоят в одном из двух соотношений

- Отношение строгого упорядочения состояний заключается в соответствии элементу множества определенного положения на числовой оси и выполнении одного из неравенств

- Отношение эквивалентности и строгого упорядочения интервалов выполняется в том случае, когда для разности двух элементов множества относительно разности двух других элементов справедливо одно из неравенств

- Отношение эквивалентности и строгого упорядочения частных подразумевает, что каждое частное от деления двух элементов множества в отношении к частному от деления двух других элементов определяется одним из выражений

Вышеприведенные соотношения, положенные в основу создания образа действительности (в области абстракции), отражающего состояние характеристик объектов, справедливы только, когда значения величин отображения принадлежат множеству положительных действительных чисел.

1.4.Решающие правила отображения ЭСО в МСО

Для формирования измерительной шкалы из множества необходимо выбрать только один элемент , который лучше всех отображает состояние а. Выбор такого

Рис.16. Математические методы, используемые в теории измерений

Рис. 17. Элементы эмпирической и математической систем отношений

Рис.18.Отображение элементов реальной области в область абстракции

элемента выполняется в соответствии с решением D таким, что .

Для решения этой задачи используют решающие правила.

1. В соответствии с первым решающим правилом выбирают наиболее вероятное значение такое, что , т.е. модальное значение.

2.В соответствии со вторым правилом выбирают среднее значение такое, что либо .

2.Третье правило предусматривает выбор в качестве отображающего элемента медианы .

Графическое изображение образов состояния а для правил решения D­_1­,D­_2­,D­_3­ приведено на рис.19. При симметричной дифференциальной функции распределения вероятности значения могут быть одинаковы.

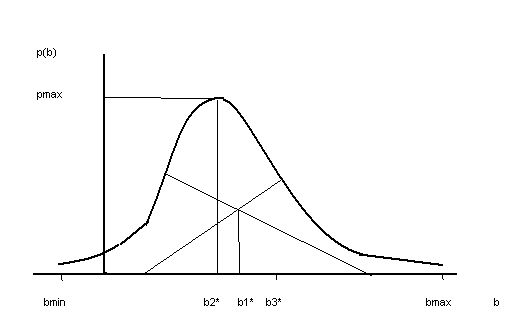
Рис.19. Графическое изображение элементов отображения в соответствии с решающими правилами