1. Постулат о волновой функции и ее смысл. Постулат о волновой функции частиц, образующих систему Сущ-ет ф-ция коорд-т и времени, используя которую можно расч-ть ве-ть обнар-я частицы в некоторой области простр-ва. Эта же ф-ция позволяет рассчитать вер-ть обнар-ния у этой частицы опред. величины P.

Сама по себе ф-ция состояния ψ не имеет физ. смысла. Смысл имеет квадрат ее модуля.

3. Постулат о средней величине энергии. Ср. значение энергии системы частиц может быть рассчитана

2. Постулат Шредингера (уравнение Шредингера) в физической химии. Позволяет опр-ть (рассчитать) ф-цию ψ

 Для ФХ особое значение имеет ситуация, когда ψ от времени не зависит

– Гамильтониан

Решения квантомеханических задач сводится к опред-ю ф-ции V в случае, когда рассчитана ф-ция V и остается решить ур-ие. Решение этого ДУ может быть найдена с точностью до пост-го множителя. Из теории спец. ф-ций следует, что решений получается несколько:

E₁ ψ₁, a ψ_1, b ψ₁, …

E₂ ψ₂, a ψ_2, b ψ₂, …

Еще одна особенность ψ­₁, ψ₂ и т.д. явл-ся то, что

Какому-либо знач-ю энергии может соотв-ть несколько ф-ций ψ, отлич-ся друг от друга не только пост. множителями. В этом случае сост-е с энергией E_i наз-ся вырожденным. Если этих ф-ций 2 => дважды вырожденным и т.д.

4. Постулат Паули (принцип запрета Паули). В одном состоянии не может быть двух частиц, обладающих одними и тем же значениями четверки квантовых чисел n, l, m_l, m_s.Это ограничение характерно для частиц, называющихся фермионами и подчиняется статистике Ферми-Дирака и облад-щих ½ спинами. Для этих частиц ф-ция состояния как решение ур-я Шредингера (УШ) должна быть ассиметрична, т.е. при перестановке 2х электронов, состояние которых описывает эта ф–ция, волновая ф-ция должна менять значение. В то же время решением УШ явл-ся еще одна ф-ция, тоже непрервная, так же однозначная, так же симметрична. Она описывает поведение частиц, называемых базонами.

5. Постулат о самосопряженном операторе. Каждой динамической переменной классической физики (координате, импульсу, энергии и т.д.) в квант-й механике соотв-т опред-ный линейный самоспряж-й оператор.

Линейный оператор

C₁ и С₂ – константы

– линейный

Самосопряженный, если

7. Первое приближение при решении уравнения Шредингера. Заключается в том, что при расчете ф-ции сост-я электронов точное значение Гамильтониана, включающее внешнее, внутр-е и электростат-е взаимод-е заменяют H, учит-щее только электростат.

Под H_внеш понимается возд-вие на систему эл-нов внешних полей. Принебречь можно, т.к. в пределах произв-х установок и полеземли, и гравитация примерно неизменны и сравнительно легко учит-ся поправки. Под H_внутр понимается взаим-вие м/уядрами, обр-щими молекулу. Там действ-т молекул-ные силы, достаточно стабильные, слабо подверг-ся возд-вию электронов.

8. Второе приближение при решении уравнения Шредингера (Оппенгеймера). Адиабатическое приближение Борна-Оппенгеймера. Масса ядер в 10³-10⁵ больше, чем масса всех электронов => можно не учитывать изменение расст-я м/у ядрами в процессе хим. Превращений. Можно не учитывать их колебания т.е. расстояние м/у ядрами R входит в расчетное соотношение как параметр или как const.

6. Постулат о суперпозиции состояний. Если частица может нах-ся в сост-ях ψ₁ и ψ₂, то линейная суперпозиция двух состояний, в которых может нах-ся частица - лин. суперпозиция двух состояний

С₁ и С₂ нах-ся из условия нормировки:

9. Третье приближение при решении уравнений Шредингера (Хартри - Фока). Это приближение заключается в том, что Хартри предложил исследовать поведение отдельного электрона, т.е. рассчитывать ф-цию его состояния, не учитывая взаимодействие этого электрона с каждым из других эл-нов в отдельности, а вместо этого ввести в Гамильтониан некоторое эффективное поле, усреднено учитывающее действие всех эл-нов на исслед-й электрон. Это эффективное поле можно опред-ть экспер-но, тем более что любая величина для исслед. эл-на рассчит-ся в среднем, а в дальнейшем если такое приближение окажется грубым, его можно уточнять и уточнять. Используя приближение Х-Ф определяют ф-цию состояния для каждого из эл-в системы H_iφ_i=Eφ_i

Приближение Хартри учитывает пространственные координаты электрона, связанные с его орбитальным моментом => определяемая ф-ция состояния наз-ся орбитальной.

11. Метод молекулярных орбиталей и линейной комбинации атомных орбиталей при анализе основного состояния молекулы. Для определения волновых ф-ций не отдельного атома, а системы атомов, объединенных в молекулы, когда эл-ны нах-ся в поле, не обладающим сферич-й симметрией, Ф определяет 2 метода: метод Валентных связей и метод молекулярных орбиталей. Оба метода дают приближения. В одних ситуациях применяется один метод. в других – другой. В ММО все орбитали рассчит-ся для всей системы ядер. Т.е. для каждого из эл-нов, входящих в состав молекулы в гамильтониан включают энергию взаимодействия эл-нов с 1, 2, 3 и т.д. ядром. В одной из разновидностей ММО после того, как записан H-ан проверяют на пригодность в качестве ф-ций состояния ф-цию, составленную из атомных орбиталей отд. атомов:

Метод линейн-х комб-ций атомных орбиталей (МЛКАО) – одна из ММО. Ф-ция состояния молекул-х орбиталей строятся по привед-й схеме. - ф-ция состояния всей молекулы. Энергия молекулы опред-ся по формуле ; – кол-во электронов; - энергия эл-на на i-ой орбите

10. Четвертое приближение при решении уравнения Шредингера (средней энергии). Т.к. в ФХ большое значение имеет ср. энергия системы и методы ее опред-я (именно оно опред-т напр-е хим. реакций) в квантовой химии разработаны методики опр-я ср. значения энергии системы

Если ф-цию состояния представить в виде линейн-й комб-ции ф-ций сост-я отд-х атомов, то рассчитать ср .значение энергии системы можно методом вариаций кэф-в C₁ … C_N (вариационное Т). Один из коэф-в, например C_i ,считается переменной величиной, ε – тоже, а ост-ное – const. => 1е ур-ние

Дальше дифф-ем по след. const, меняем индекс . Всего будет n уравнений. Решая эти ур-я можно получить набор значений ε. Min из этих значений рассм-ся как энергия основного состояния системы, остальные – как возбужд. состояний системы (выделение основного состояния необходимо потому, что любая система -> min своей энергии, а именно такими состояниями занимается ФХ). Далее ε_min подставляем в 1, 2, …, n ур-ния, находим соотношение м/у C₁, C₂, и C_n. Полученные значения (C₁, C₂, …) подставляем в ур-ние нормировки

Находим численное значение C₁, C₂, и C_n. Найти соотношение м/у C₁, C₂, и C_{n означает,} что все C_i можно выразить ч/з C₁, C₂, и C_n.

12. Метод валентных связей при анализе основного состояния молекулы. Для определения волновых ф-ций не отдельного атома, а системы атомов, объединенных в молекулы, когда эл-ны нах-ся в поле, не обладающим сферич-й симметрией, Ф определяет 2 метода: метод Валентных связей и метод молекулярных орбиталей. Оба метода дают приближения. В одних ситуациях применяется один метод. в других – другой. В методе ВС предполагается, что при объединении атомов в молекулы, атомные орбитали каждого из атомов практически не меняются, за исключением атомных орбиталей нескольких эл-нов, с помощью которых атомы вступают во взаимодействие. Как правило это наружные электроны атомных оболочек.

13. Основные положения при построении электронной конфигурации. Совокупность МО молекулы, занятых эл-нами наз-ся электронной конфигурацией молекулы. Не все орбитали, доступные эл-нам могут быть заняты. Одни будут заняты как правило, другие буду заняты при наличии внешнего излучения. При этом выполн-ся следующие принципы:

1) наименьшей энергии. Каждый новый электрон занимает в молекуле незант-ую орбиталь с min энергией

2) принцип Паули. На одной орбитали могут нах-ся 2 электрона с различными спинами.

14. Критерии выбора атомного базиса при построении электронной конфигурации. Набор атомных орбиталей, с помощью которых рассчит-ся МО должен отвечать опред. требованиям:

1) выбранные атомные орбитали должны обеспечивать хорошее эксперим-е соотв-вие вероятностных хар-к, полученных для молек-х орбиталей, рассчит-е с исп-нием выбранных атомных орбиталей.

2) атомные орбитали, выбранные для построения атомных орбиталей, должны обеспечивать аналит-й расчет всех интегралов, фигурирующих в рассчетх соотношениях.

3) полное число атомных орбиталей, исп-х при расчете атомных орбит, не должно быть слишком большим.

15. Условия успешного комбинирования атомных орбиталей в молекулярную орбиталь. Для успешного комбинирования атомных орбиталей в молекулярную орбиталь желательно чтобы:

1) энергии выбранных АО были сравнимы по величине

2) электр-е облака. Хар-щие плотность вер-ти нах-ния эл-нов вблизи ядра, относящ-ся к сосед-щим атомам, должны max перекрываться

3) атомные орбитали, выбранные для построения МО должны, обладать одинаковой симметрией.

31. Тепловой эффект реакции и закон Гесса. Раздел хим-й ТД, посвящ-й исслед-ю тепл-х эфф-в хим-х реакций, фазовых переходов, процессов растворения вещ-ва, наз-ся термохимией. При хим-х реакц-х происходит перестройка электр-х оболочек, разрыв хим. связей и появление новых, что ведет либо к поглощению энергии из окр. среды, либо к выделению в ок-щую среду. Можно показать, что для большинства процессов термохимии выполняется след-е положение (правило):

1) процессы протекают необратимо при p=const или V=const.

2) при протекании термохим. процессов не совершается никакой другой работы, кроме процессов расширения.

3) T исх-ных продуктов хим-й реакции и конечных продуктов равны.

В этом случае выполняется соотношение, справедливое для реальных газов:

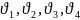– стехиометрические коэф-ты

33. Второе следствие закона Гесса. Тепловой эффект реакции и теплота образования вещества. Тепловой эффект ХР равен разности суммы теплот продуктов реакции и суммы теплот образования исх-х вещ-в. Теплоты образования – кол-во тепла, поглощаемая или выделяемая при образовании 1 моля i-го вещ-ва из простых вещ-в, взятых в ТД устойчивом состоянии при T=298K и P = 1 атм.

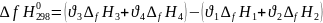
Как и теплоты сгорания, теплоты обр-ния определены и табулированы.

32. Первое следствие закона Гесса. Тепловой эффект реакции и теплота сгорания. Закон Гесса говорит, что в результате протекания хим. реакции при норм. условиях (T=298⁰K и P=1.012 * 10⁵Па), закон Гесса имеет 2 формы: тепловой эффект реакции = разности теплот сгорания исходных веществ и теплот сгорания продуктов реакции. До высших окислов в среде O₂ при P = 20-30Па сжигание происходит в калориметрических бомбах. В этом Q эффект реакции можно определить след. образом:

– тепловой эффект реакции; - теплота сгорания компонента А₁ ; - стехиометрический коэфф-т исходного ур-ния и т.д. Значение в настоящее время можно определить с достаточно высокой точностью. Они определены и табулированы.

48. Третий закон термодинамики и постулат Нернста.

Из этих соотношений => для определения T зависимости необх-мо знать:

1) Т зависимость

2) знать необх-мо в диапазоне от 0 до P

3) необх-мо знать const интегр-ния 1 ур-ия

Определить эти соотношения можно из эксп-та при известной const v реакции. Гораздо простым решением явл-ся метод, разраб-й Нернстом и основанный на

Это справедливо только для крист. в-в.

4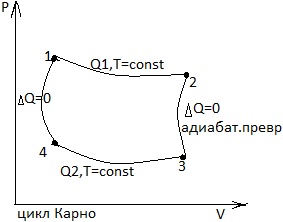 9. Основные следствия постулата Нернста. Метод, определения Т зависимости, разраб-й Нернстом и основанный на справедлив только для крист. вещ-в. Из него следует ряд полезных следствий:

1) для крист. в-в пределом этого соотн = 0

2) => при T->0 тепловой эффект и изменение теплоемкости от T не зависят

3) для процессов, сопровождающих взаимод-е крист. в-в это отношение записано не только для Гиббса, но и для энтропии

Необходимо отметить, что это соотношение справедливо только для крист. в-в. Для растворов не выполняется.

4) для процессов, сопровождающих взаимод-е крист. в-в,

5)

где

j – истинная хим. постоянная

В целом III закон ТД с учетом соотношением Нернста и приведенных следствий м/б сформ-на след. образом:

Энтропия любого бездефектного индивидуального кристалл. Вещ-ва при 0⁰K=0

S=k*lnΩ

k – постоянная Больцмана

Ω – статистич. вес, т.е. число микросостояний, посредством которых реализ-ся данное макросост. То, что при S при 0⁰K=0, означает, что в индивид. крист. бездефф. в-вах равнов. состоянием м/б реализовано только одним способом.

36. Характер функции при S,V=const. T при S,V=const-мера возрастания U, сопровождающийся ростом S при V=const. P при ,V=const-мера убыли U, сопровождающаяся при S=const. вывод: S,V=const

37. Характер функции при S,P=const. dH=dU+pdV+Vdp⇒dH=TdS+Vdp ; вывод: S,P=const

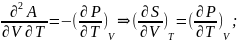
38. Характер функции при T,V=const. A-Энергия Гельмгольца. Вывод: T,V=const ;

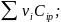
34.Зависим. теплового эффекта от Т. Уравнение Кирхгофа. Проблема состоит в том, что тепл. эфф. нужно рассчитывать не только при норм. Т, но и при повышенной Т. Этой проблемой занимался Кирхгоф. ; = (1) ; (1)-уравнение Кирхгофа. Теплов. эфф. может менять свой знак. ; 1)3 2)2 3)

Д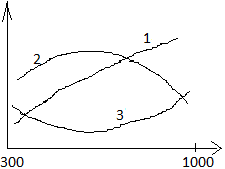 ля определения 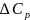используют экстраполяцию теплоемкости с помощью 3 членов: А+ВТ+С или А+ВС+ С . В последнем соотношении вместо табл. соотн. используют ∆r . Для упрощения расчетов используют усредн. значение теплоемкостей, заданных в определенном интервале Т:

35. II закон ТД. Самопроизвольные и несамопроизвольные процессы. Энтропия и ее изменение. II ЗТД определяет невозможность создания вечного двигателя 2-го рода: Q→A. Тепло, переданное рабочему телу, превращает тепло в работу, частично должно быть передано холодильнику 1-2-изотерма( ); 2-3-адиабата ∆Q=0 расширение;3-4-изотерма ( );4-1-адиабата ∆Q=0 сжатие. η= ; η= ; (*). Все эти рассуждения касаются квазистат. процессов, сопровождается изменением P и V, изменяющихся небольшими порциями, приближая состояние системы (СС) к равновесной. Если система выйдет из равн-я, то (*) не будет выполняться. Для подынтегр. выражения было предложено опред-е энтропии. dS= справедливо, когда система соверш. равна работе увелич. U системы, т.е Энтропия явл-ся экстенсивной ТД функцией. Если система состоит из атомов, то . Для квазистат. процессов в изолирован.системах 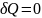при U,V=const. В этом случае при U,V=const, для нестац. процессов .В то же время в отдельн. частях изолированной системы S может ↑, а в других ↓. Но в целом наличие участков ↑ и ↓ энтропии означает, что система в нестационарн. состоянии S или S ,в итоге суммарная энтропия растет. а)

39. Уравнение Гиббса-Гельмгольца.

ТД соотношения, устанавливающие связь между внутренней энергией U и энергией Гельмгольца (свободной энергией F) или между энтальпией H и энергией Гиббса (свободной энтальпией G): ,H=G-T Ур-ие (1) следует из определения энергии Гельмгольца F=U-TS и выражения для энтропии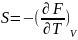 . Ур-ие (2) - из определения энергии Гиббса G=H-TS и выражения для энтропии S=- . Ур-ние (1) позволяет по энергии Гельмгольца F(T, V)найти внутр. энергию U(T, V)и, следовательно, теплоёмкость при пост. объёме. Ур-ние (2) позволяет по энергии Гиббса G(T, P) найти энтальпию H(T, P) и, следовательно, теплоёмкость при P=const. Маx работа, к-рую может совершить система в тепловом контакте с окружающей средой удовлетв. ур-ию Гиббса-Гель. . Эта max работа за вычетом работы против сил давления P(V₂-V₁) (максимальная полезная работа) ,удовл.ур.Гиббса-Гель.:

40. Характер функции при Р,Т=const. ; Вывод: Р,Т=const, const ;