14. Расчет условно центрально сжатых элементов
Расчет элементов неармированных каменных конструкций при центральном сжатии следует производить по формуле N ≤ mg φ RA, (10)
где, N — расчетная продольная сила; R — расчетное сопротивление сжатию кладки, определяемое по табл. 2 — 9; φ — коэффициент продольного изгиба, определяемый по п. 4.2; а — площадь сечения элемента; т — коэффициент, учитывающий влияние длительной нагрузки и определяемый по формуле (16) при е0g = 0.
При меньшем размере прямоугольного поперечного сечения элементов h ≥ 30 см (или с меньшим радиусом инерции элементов любого сечения i ≥ 8,7 см) коэффициент тg следует принимать равным единице.
Коэффициент продольного изгиба φ для элементов постоянного по длине сечения следует принимать по табл. 18 в зависимости от гибкости элемента
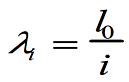(11)
или прямоугольного сплошного сечения при отношении
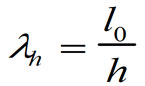(12)
и упругой характеристики кладки α, принимаемый по табл. 15, а для кладки с сетчатым армированием — по формуле (4). В формулах (11) и (12): l0 — расчетная высота (длина) элемента; i — наименьший радиус инерции сечения элемента; h — меньший размер прямоугольного сечения.
15. Расчет внецентренно сжатых элементов в случае малых эксцентриситетов
Внецентренно сжатыми называются элементы, в которых направления сжимающего усилия N не совпадает с осью, проходящей через центр тяжести сечения, а находится на некотором расстоянии от него, называемом эксцентриситетом. При ξ > ξR малые эксцентр-тах разрушение начинается со стороны сжатой зоны, в отличие от первого случая, где разрушение происходит по принципу Лолейта, с растянутой арматурой АS.
В случае 2 арматура АS может быть и растянутой и сжатой при этом напряжение в ней δS может отличаться от расчетного сопротивления. Величина фактических напряжений δS для бетона классов В30 и арматуры А2 и А3 определяется по эмпирической формуле: δS = RS (2(1 – x/h0) / (1 - ξR) – 1), при х = ξR h0 δS = RS, а при х = h0 δS = RSC, Для случая малых эксцентриситетов основное условие прочности 1 остается без изменений, а в условии 2 N ≤ Rb bx + RSC ASC - δS (±AS ) ,где - растянуто, + сжато.Учет гибкости. Рис. Гибкие элементы под действием момента произвольной продольной силы N прогибаются, начальный эксцентриситет возрастает, что снижает несущую способность. Расчет таких элементов следует вести по дефор-й схеме с учетом ползучести бетона и наличии трещин в растянутой зоне.
16. Расчет внецентренно сжатых элементов в случае больших эксцентриситетов
При расчете сжатых элементов всегда учитывается случайный эксцентриситет, который вызван неоднородностью бетона, отклонением размеров, неточностью приложенной нагрузки и т.д. Его принимают не менее 1/600 l (l – длина участка) Общую длину эксцентриситета получают: l0 = l0N + l0сл , l0N = M / N , l0сл – случайный. Характер работы внецентренно сжатых элементов зависит от величины эксцентриситета.
При больших эксцентриситетах работа элемента напоминает работу элемента изгибаемого с двойным армированием. В части сечения расположенной ближе к силе N наблюдается сжатие, а с другой стороны сечения растяжение. В сжатой зоне работают два материала – арматура воспринимает усилие RSC ASC, а бетон Rb bx; в растянутой зоне всё растяжение воспринимает арматура AS , при этом напряжение в ней может достигать расчетного сопротивления на растяжение RS. Такое состояние наблюдается, когда х / h0 = ξ ≤ ξR большие эксцен-ты. Основное условие прочности для случая больших эксцентриситетов состоит в том чтобы расчетный изгибающий момент от внешней продольной силы:NL ≤ RSCASC (h0 – a’)+Rb bx (h0 –0,5x) не превысил изгиб момента, воспринимаемого сжатой арматуры и сжатым бетоном относительно оси, проходящей через центр тяжести растянутой арматуры. Кроме того должно соблюдаться равновесие внешних и внутренних сил на продольную ось элемента. N ≤ Rb bx + RSC A’SC - RS AS.