2Представление цифровых сигналов и систем в частотной области. Частотная характеристика.

Синусоидальная последовательность и последовательность типа комплексная экспонента являются собственными функциями ЛИВ систем, поэтому отклик будет иметь ту же форму.

Рассмотрим специальный класс входных последовательностей (комплексная экспонента). Покажем, что она является собственной функцией ЛИВ системы дискретного времени, т.е. проходя через ЛИВ систему комплексная экспонента не меняет свою форму, а меняет модуль и фазу.

Таким образом, для выбранного класса входных последовательностей выход совпадает со входом с точностью до комплексного множителя, который выражается через импульсную характеристику

- частотная характеристика ЦФ.

, отсюда ясно, что описывает изменение комплексной амплитуды комплексной экспоненты, как функции частоты ω.

Свойства частотной характеристики:

1)Частотная характеристика – это непрерывная функция частоты ω, причем периодическая с периодом 2П. Обычно ее рассматривают на отрезке

2)Частотная характеристика может быть представлена:

Если импульсная характеристика действительна, то модуль частотной характеристики четная функция, а аргумент нечетная функция частоты ω и наоборот.

Т.к. функция периодическая, то

Пример: Пусть дан ЦФ со следующей характеристикой:

По определению:

Импульсная характеристика представляет собой коэффициенты Фурье периодической функции , т.е. .

Рассмотрим произвольную числовую последовательность :

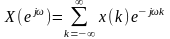- прямое преобразование Фурье числовой последовательности x(n).

Тогда: - обратное преобразование Фурье числовой последовательности x(n).

Билет 10.

1Эффект наложения спектров. Частота Найквиста

Частота Найквиста — в цифровой обработке сигналов частота, равная половине частоты дискретизации. Названа в честь Гарри Найквиста. Из теоремы Котельникова следует, что при дискретизации аналогового сигнала потерь информации не будет только в том случае, если спектр (спектральная плотность) сигнала равна или выше частоты Найквиста. В противном случае при восстановлении аналогового сигнала будет иметь место наложение спектральных «хвостов» (подмена частот, маскировка частот), и форма восстановленного сигнала будет искажена. Если спектр сигнала не имеет составляющих выше частоты Найквиста, то он может быть (теоретически) продискретизирован и затем восстановлен без искажений.

Маскировка частот

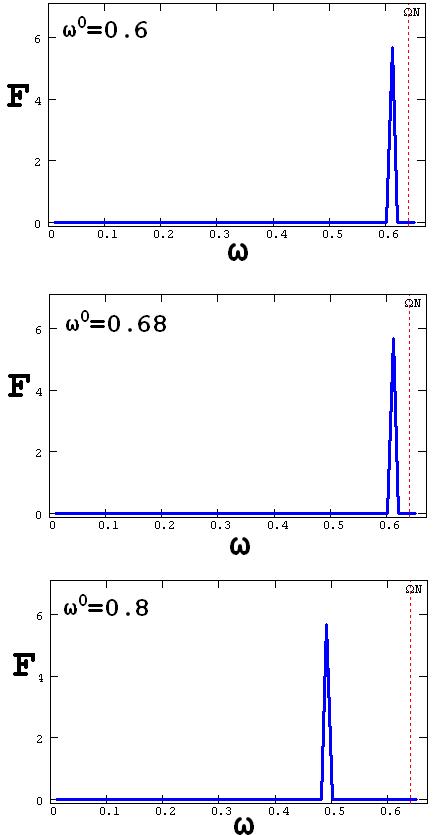
Классический пример ошибочного расчета Фурье-спектра связан

с возможным присутствием в сигнале гармоник с частотой,

превышающей частоту Найквиста. Рассмотрим выборку, для

которой Ω^N=0.64 (см. рис. 61-63). На рис. 64 приведена иллюстра-

ция эффекта, называемого маскировкой частот. Он содержит

расчет спектров трех различных синусоидальных сигналов с

разной частотой ω0, значение которой находится вблизи частоты

Найквиста, которая на всех графиках выделена пунктирной

линией.

Первый спектр сигнала (сверху) с частотой ω0_, меньшей частоты

Найквиста ΩN, вычислен верно, а вот два остальных спектра

(в центре и внизу) показывают, что, если ω0 превышает частоту

Найквиста, то в спектре начинают присутствовать

неправильные, «лишние» пики. На самом деле, пик спектра

для обоих случаев

должен располагаться справа от пунктира.

Артефакты спектра связаны, конечно, с нехваткой числа отсчетов

для представления

высокочастотных гармоник с достаточной информативностью.