2Устойчивость и физическая реализуемость цифровых лив-систем.
Устойчивым ЦФ называется фильтр, в котором каждый ограниченный вход создает ограниченный выход.
ЦФ устойчив тогда и только тогда, когда его ИХ абсолютно суммируема.
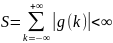
Доказательство:
Пусть
– вход ограничен для всех n,
тогда
Докажем обратное
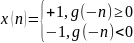
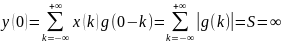
Физически реализуемый фильтр – это фильтр, у которого изменения на выходе не опережают изменения на входе.
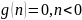
ЦФ физически реализуем тогда и только тогда, когда его ИХ равна 0 при n=0.
Пусть задан фильтр с ИХ:
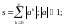второе
условие – устойчивость
Билет 7.
1Спектр типовых импульсных сигналов
Дельта функция (Функция Дирака).
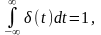т.е.
площадь
.
Спектральная
плотность δ(t):
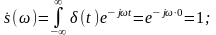
В
спектре присутствуют все частоты (по
косинусам в нуле =1 вблизи нуля компенсируют
друг друга)
2.Единичный скачок 1(t):
3.Прямоугольный импульс:
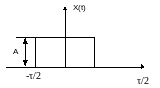
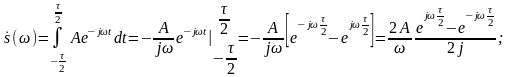
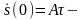площадь
под кривой сигнала.
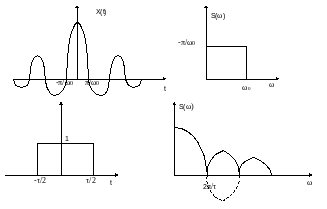
Спектр прямоугольного сигнал:
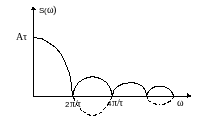
Найдем нули:
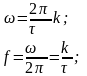
Под шириной спектра, как правило, понимают, либо полосу частот до первого нуля, либо полосу частот, на которую приходится 90% энергии переносимой сигналом.
Ширина спектра:
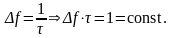
Чем уже импульс, тем шире его спектр.
Доказано что:
Точность измеряемой частоты тем выше, чем больше время измерения.
Сигнал типа:
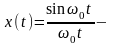сигнал
с ограниченным спектром.
2Линейные разностные уравнения с постоянными коэффициентами.
Важным подклассом ЛИВ – систем являются фильтры, для которых вход x(n) и y(n) удовлетворяют линейному разностному уравнению n-го порядка с постоянными коэффициентами вида:
Вводя новые ограничения, запишем:
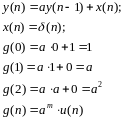ИХ
фильтра с таким уравнением бесконечна
Изобразим структурную схему фильтра, описанную этими уравнениями:
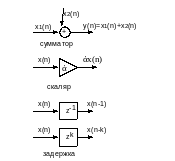
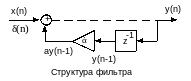
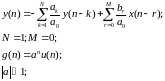
В общем случае ЦФ может иметь импульсную характеристику, как конечной, так и бесконечной характеристики. Такие фильтры называются БИХ и КИХ-фильтры.
Тогда:
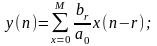
Пример: М=1.
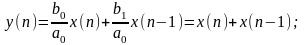
Структурная схема фильтра:
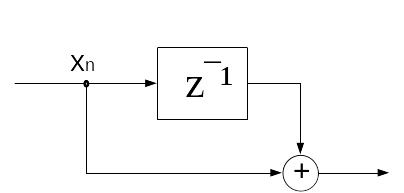
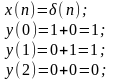
Найдем импульсную характеристику:
Билет 8.
1Теорема о спектрах. Преобразование спектров в линейных цепях.
Оператор L линейный, если
Теорема1. Спектр суммы
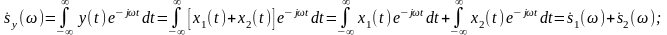
Теорема 2. Спектр производной.
Сигнал x(t) имеет спектр s̀(ω). x(t)↔ s̀(ω).
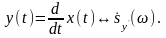
Представим x(t) интегралом Фурье:
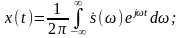
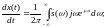
Теорема 3. Спектр интеграла.
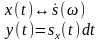
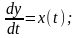
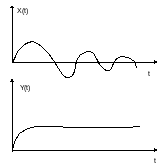
Теорема 4. Произведение двух сигналов.
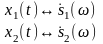
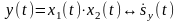
По определению:
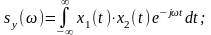
Представим x1(t) интегралом Фурье:
здесь
интегрирование по ню
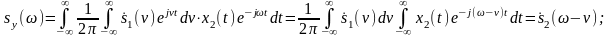здесь
должен быть интеграл, который далее
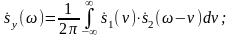(1)
Интеграл (1)
называется сверткой комплексных функций
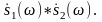
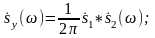
При свертке одна из двух функций берется в том виде, в каком она исходно задана. А для другой изменяется направление оси абсцисс. Производится сдвиг функций по этой оси на некоторое значение аргумента ω. Затем эти две функции перемножаются и произведение интегрируется. Т.е. находится площадь под кривой произведения. Полученный интеграл (число) и является значением свертки для заданного значения аргумента ω.
Теорема 6. Спектр свертки сигнала.
