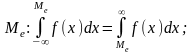1Ряд Фурье. Три формы.

Постановка задачи: Пусть x(t) любой периодический сигнал: x(t)=x(t+T);

Первая гармоника сигнала: ω1=2π/Т;

Необходимо разложить сигнал по системе базисных функций:

{φk(t)}={сos k ω1t, sin k ω1t}; (*)

Используя критерий сходимости в среднеквадратическом. Всякий, с несущественными для практики математическими ограничениями (условиями Дирихле), периодический сигнал x(t) с периодом Т=2π/ ω1, может быть представлен рядом по тригонометрическим функциям:

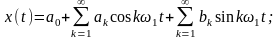(1) – синусно-косинусная форма ряда Фурье

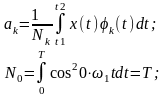
Если коэффициенты ряда (1) найдены по формулам (2), то ряд (1) называется рядом Фурье.

Вещественная форма представления ряда Фурье:

(3)

{ak,bk}↔{ck,ψk};

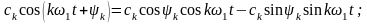
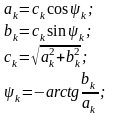
Комплексная форма ряда Фурье:

, где 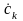- комплексная амплитуда.

Зная формула Эйлера:

Тогда выражение (3) примет вид:

Для общности обозначим:

{ck} – спектр амплитуды сигнала x(t);

{ψk}- спектр фаз сигнала x(t);

{ }- комплексный спектр сигнала x(t);

{ }- система базисных функций в виде комплексных экспонент;

{ak,bk}↔{ck…,ψk};

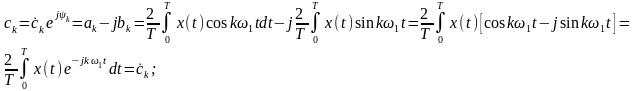
2Цифровые лив-системы. Импульсная характеристика. Свёртка числовых последовательностей.

Цифровые системы (ЦФ) определяются математически, как однозначное преобразование или оператор, отображающий входную последовательность в выходную.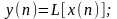

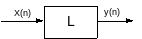В зависимости от ограничений, накладываемых на оператор L различают несколько классов ЦФ.

Первый класс линейных цифровых фильтров определяется принципом суперпозиций, является откликом .

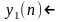
_{система линейна тогда, когда}

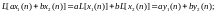
Второй класс инвариантных к сдвигу ЦФ определяется следующим свойством:

;

;

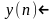
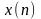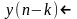
нестареющая система – это система с постоянными параметрами

g(n) – отклик системы на единичный импульс

- импульсная характеристика фильтра.

Отклик фильтра на произвольную последовательность обозначенную y(n).

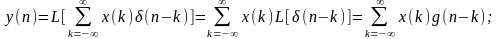
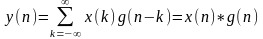- свертка.

Импульсная характеристика полностью характеризует фильтр.

Легко показать, что:

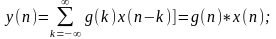
Рассмотрим варианты каскадного включения двух ЦФ.

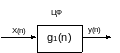
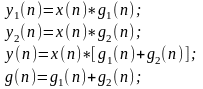
Пример вычисления свёртки

Каждая последовательность 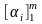, у которой частное отношение двух соседних членов постоянно

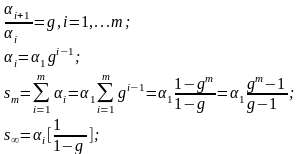
Рассмотрим ЦФ с импульсной характеристикой вида:

здесь очевидно, что а в степени n

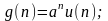
Найдем реакцию на входной сигнал вида:

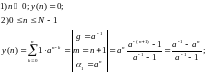
последовательность возрастает

последовательность убывает

Билет 6.

1Оценивание распределения параметров генеральной совокупности методом квантилей

Е – случайные события. Ω – эксперимент.

- достоверное событие.

- невозможное событие.

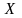- случайная величина – это величина, которая может принять то или иное значение из возможных.

- область возможных значений.

Квантиль – значение, которое заданная случайная величина не превышает с фиксированной вероятностью. Единственный корень уравнения

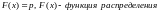
- функция распределения вероятностей.

это теоретический квантиль.

выборочный квантиль

Из ГС извлекаем выборку, упорядочиваем элементы в порядке возрастания. далее строим ф-ю распределения

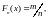
n-объем выборки, m- число элементов меньше или равных выборочн. фун-ии распред.

Выборочным квантилем уровня р наз-ся единственный корень уравнения

Ent – целая часть от произведения

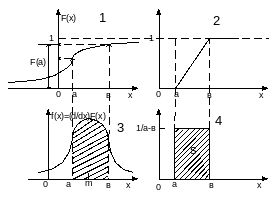
Св-ва оценок:

они состоятельны

они ассиметричны и нормальны

этот метод не гарантирует несмещенность и эффективность

1. Интегральный закон распределения.

2. 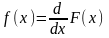- плотность распределения вероятности.

3.

4. Дифференциальный закон распределения. 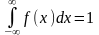- условия нормировки.

Среди числовых характеристик выделяют характеристики положения и рассеивания. К характеристикам положения относят m, M0, Me (мат. ожидание, мода и медиана).

1. 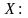- мат. ожидание.

x1	x2	x3
p1	p2	p3

2. 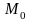- мода.

Это значение, которое встречается максимальное число раз

3. 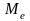-медиана.