2. Оценивание параметров распределения генеральной совокупности методом максимального правдоподобия.

Наиболее мощный метод, наиболее полно учитывает информацию несомую выборкой.

Имеем ГС ;

Извлекается выборка:

Составляется функция правдоподобия:

Функция правдоподобия характеризует вероятность появления именно той выборки, которая получена в эксперименте. Если необходимо по выборке оценить вектор θ, то естественно взять в качестве оценок , такие, которые бы имели максимальную вероятность.

Из соображений удобства вычисляют функцию правдоподобия.

Рассмотрим ее логарифм:

Для нахождения оценок, находятся частотные производные.

Пусть имеем нормальную ГС:

ГС

Перейдем к логарифмической функции:

- оценка максимального правдоподобия мат. ожидания нормально распределенной ГС.

- выборочная средняя.

Проверка на несмещенность:

1) - доказать.

- оценка несмещенная.

2)Состоятельность оценки.

3)Требования эффективности.

Получена эффективная оценка.

Пример:

P – вероятность появления событий Е в случайном эксперименте Ω. Пусть проведено n отсчетов, событие Е произошло в ν случаях.

Доказать, что частота событий - есть оценка максимального правдоподобия.

Введем вспомогательную величину

X	1	0
вер	p	(1-р)

Билет 4

1Аппроксимация сигналов системами ортогональных функций

Постановка задачи:

Задан сигнал x(t) на отрезке времени t=[t1,t2], который необходимо аппроксимировать x*n(t)=∑аkφk(t). Задана система базисных функций: {φk(t)}. Критерий сходимости: среднеквадратический.

Эта задача решается наиболее просто, если система базисных функций {φk(t)} ортогональна.

Система базисных функций {φk(t)}, называется ортогональной на отрезке [t1,t2], если:

1)

2)

Nk – называется нормой базисной функции. (здесь надо поставить квадрат во всех Nk, иначе это квадрат нормы)

Если для всех k Nk =1, то такая система базисных функций называется ортогональной и нормированной (ортонормированная).

Запишем критерий сходимости в среднеквадратическом:

Необходимо найти такие аk, чтобы Q→min для данного n.

Найдем частную производную от Q по aj :

В некоторых случаях удобно использовать базисные системы функций ортогональных с весом {ψk(t)}.

Система называется ортогональной с весом, если:

От функции ортогональной с весом легко перейти к функциям ортогональным без веса: {ψk(t)}→ {φk(t)}.

Необходимо найти ск:

2Типовые числовые последовательности

1. Единичный импульс:

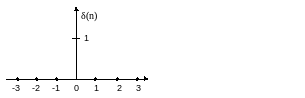
2. Единичный скачек:

3.Действительная экспоненциальная последовательность:

Гармоническая последовательность:

4.Комплексная экспоненциальная последовательность:

Последовательность x(n) называется периодической с периодом N, если x(n)=x(n+N) для всех n.

Рассмотрим пример:

Косинус – периодическая функция.

При k=1,ω0N=2π.

Тогда - целое число.

Пусть такое, что - рациональное число.

Пример:

Пусть - иррациональное число. У такой последовательности периода нет.

Параметр будем называть частотой гармонической последовательности или комплексной экспоненты независимо от того являются ли эти последовательности периодическими.

Будем рассматривать - , все остальные значения не приносят новой информации, т.к. n целое число.

Рассмотрим непрерывный гармонический сигнал:

Пусть

Энергия числовой последовательности:

Произвольная последовательность:

Билет 5