2 Спектры непериодических сигналов. Интеграл Фурье.
Непериодический сигнал можно представить как частный случай периодического сигнала, при условии, что период сигнала стремится к бесконечности.
(0)
спектральная
плотность амплитуд.
интеграл
Фурье.
Формула (1) называется прямым преобразованием Фурье, а формула (2) обратным преобразованием Фурье.
Сравнивая формулы (2) и (0) можно записать:
Это амплитуда, приходящаяся на узкую полосу частот.
Перепишем (1) в виде:
модуль
спектральной плотности.
аргумент
спектральной плотности.
и
вещественная
и мнимая часть комплексной функции.
Рассмотрим по (3) формуле два случая:
1.x(t)-четная функция.
Спектральная
плотность чисто вещественная.
2.x(t)-нечетная функция.
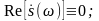Спектральная
плотность чисто мнимая.
Пусть мнимая часть сигнала x(t)=0.
комплексно
сопряженные функции.
Билет 19.
1. Передаточная функция цифровых лив систем
- передаточная функция фильтра.
В общем случае для устойчивого и физически реализуемого ЦФ область сходимости передаточной функции будет включать единичную окружность и всю z-плоскость вне окружности, включая z=∞.
Область сходимости не содержит полюсов, значит для устойчивости надо, чтобы все полюса передаточной функции лежали внутри окружности
Как известно ЦФ описывается разностным уравнением n-го порядка:
Воспользуемся свойством линейности:
Воспользуемся свойством сдвига последовательности:
Рассмотрим пример:
Пусть необходим ЦФ не пропускающий постоянную составляющую.
Возьмем z-преобразование от левой и правой части равенства:
2. Круговой сдвиг последовательности. Круговая свёртка
Круговой сдвиг последовательности.
Изобразим на рисунке следующие 4 последовательности:
Сравнение показывает, что x1(n) – не соответствует линейному сдвигу x(n).
Для трактовки такого сдвига представим, что последовательность конечной длины x(n) расположена на поверхности цилиндра в N точках. При движении по поверхности цилиндра наблюдаемая последовательность будет периодической последовательностью x̃(n). При этом линейный сдвиг последовательности x̃(n) соответствует вращению цилиндра. Такой сдвиг называется круговым.
Круговая свертка.
Рассмотрим последовательности:
Определим последовательность такой, что ДПФ . Длина x1 и x2 =N.
Такая последовательность называется круговой сверткой.
Круговая свертка отличается от линейной.
Основные операции линейной свертки:
x1(n) заменяют на обращенную во времени и линейно сдвинутую копию x2(n).
Суммирование значений произведений.
Последовательные значения свертки получаются, когда эти последовательность сдвигаются по отношению друг к другу.
Для круговой свертки следует представить, что одна из последовательностей расположена на поверхности в N равноудаленных точках. Вторая последовательность обращается во времени и также располагается на поверхности цилиндра в N точках. Если предположить, что первый цилиндр помещен внутрь другого, то тогда значение свертки может быть получено путем умножения значений первого цилиндра на соответствующие значения на втором цилиндре и суммированием полученных произведений, чтобы получить последовательные значения свертки. Первый цилиндр поворачивается относительно другого – это эквивалентно формированию сигнала двух периодических последовательностей, а затем получению свертки по формуле:
Пример: Даны две одинаковые последовательности в виде прямоугольного окна:
Необходимо найти: аналитически и графически.
Решение:
Графическое решение:
Для получения линейной свертки дополним последовательности x1 и x2 N- нулями, т.е. будем рассматривать N0 как 2N последовательности.
Билет 20.
