Влияние запаздывания

Уравнения, которые представлены выше, предполагают, что процессы размножения и гибели происходят одновременно и популяция мгновенно реагирует на любое изменение внешних условий. Однако в реальности это не так. Всегда имеется некоторое запаздывание, которое вызвано несколькими причинами.

Развитие любой взрослой особи из оплодотворенного яйца требует определенного времени T. Поэтому если какое-нибудь изменение в окружающей среде, например, увеличение ресурса, вызовет внезапное повышение продуктивности взрослых особей, то соответствующе изменение численности произойдет лишь по прошествии времени T. Это означает, что уравнение: 

dx/dt=f(x), (4)

где x - численность взрослых особей, следует заменить уравнением:

dx/dt=f(x_t-T) (4.1)

где x_t--T - численность половозрелых особей в момент t-T.

В реальных популяциях интенсивность размножения и гибели различны в разных возрастных группах. Например, у насекомых откладывают яйца взрослые особи, а конкуренция наиболее выражена на личиночной стадии. Такие процессы, как отравление среды продуктами метаболизма, каннибализм и т.п. в наиболее сильной степени воздействуют на ранние возрастные стадии, а их интенсивность зависит от численности взрослых особей, т.е. отрицательное влияние на коэффициент естественного прироста оказывают особи предыдущего поколения. С учетом этих обстоятельств, логистическое уравнение (3.1) перепишется в виде: 

dx/dt=x(r-x_t-T) (4.2)

Наиболее распространенное и изученное в динамике популяций уравнение Хатчинсона учитывает тот факт, что особи размножаются лишь с определенного возраста, и имеет вид:

 (4.3)

Смысл модели (4.3) заключается в том, что уровень лимитирования системы зависит не только от общей численности популяции в данный момент времени t, определяемой емкостью среды, но и от количества половозрелых особей в момент времени t-T. Еще более точное уравнение, учитывающее распределение времени запаздывания:

 

Вид функции распределения времен запаздывания w(t-s) представлен на рис. 4.

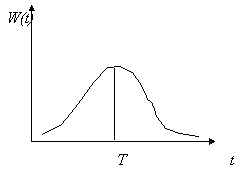
Рис.5. Модель динамики популяции с учетом распределения времен запаздывания. Типичный вид весовой функции w(t)

Такого типа уравнения могут иметь колебательные решения. Это легко проверить для простого линейного уравнения:

,

которое имеет периодическое решение   в широком диапазоне значений скоростей роста r и времени запаздывания T.

Заключение

Популяционная динамика представляет собой область математической биологии, описывающая с помощью моделей типы динамического поведения развивающихся систем, представляющих собой одну или несколько взаимодействующих популяций или внутрипопуляционных групп. Отличительной чертой биологических популяций, как и всех живых систем, является их удаленность от равновесия, использование для своего роста и развития энергии внешних источников. Это обуславливает необходимость использования для описания таких систем нелинейных моделей, позволяющих отразить основные характерные черты популяционной динамики лабораторных и природных популяций. Это - ограниченность роста, вызванная совокупностью факторов. Возможность нескольких стационарных исходов в зависимости от начальных условий роста популяции. "Зависание" системы вблизи критической границы и ее чувствительность в этой области к малым флуктуациям и индивидуальным усилиям. Запаздывание реакции системы на изменение внешних факторов. Возможность колебательных и квазистохастических режимов.. Математические результаты, полученные при изучении моделей популяционной динамики служат для практических целей управления биотехнологическими и природными системами и, дают пищу для развития собственно математических теорий.