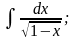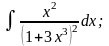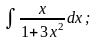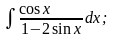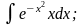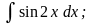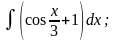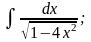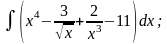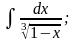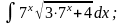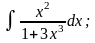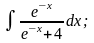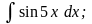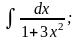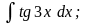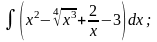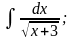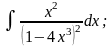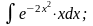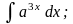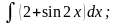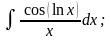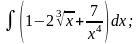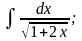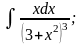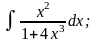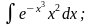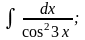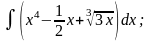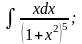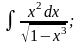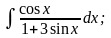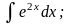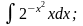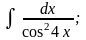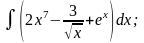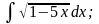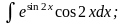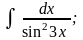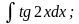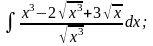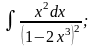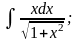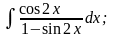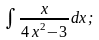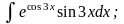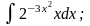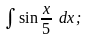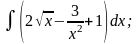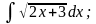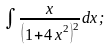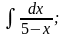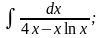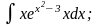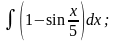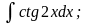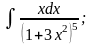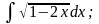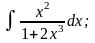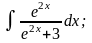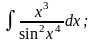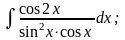Тема 5. Производная
Вычислить производные функций.
Вариант
1. 
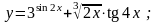
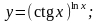
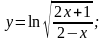
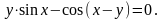
Вариант
2. 
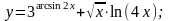
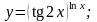
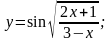
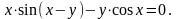
Вариант
3. 
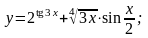
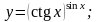
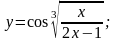
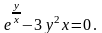
Вариант
4. 
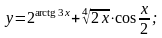
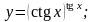
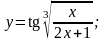
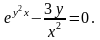
Вариант
5. 
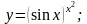
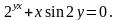
Вариант
6. 
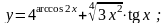
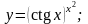
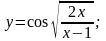
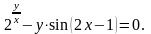
Вариант
7. 
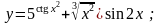
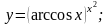
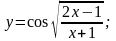
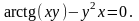
Вариант
8. 
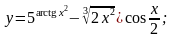
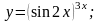
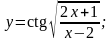
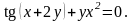
Вариант
9. 
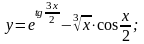
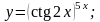
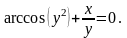
Вариант
10. 
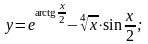
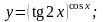
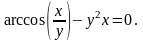
Вариант
11. 
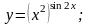
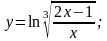
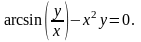
Вариант
12. 
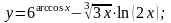
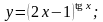
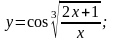
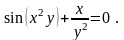
Вариант
13. 
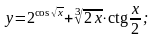
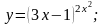
Вариант
14. 
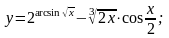
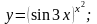
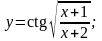
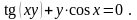
Вариант
15. 
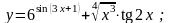
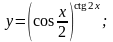
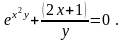
Вариант
16. 
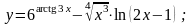
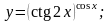
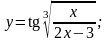
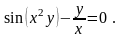
Вариант
17. 
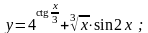
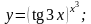
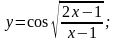
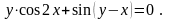
Вариант
18. 
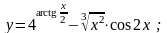
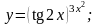
Тема 6. Исследование функций.
Вариант 1
1. Найти наибольшее и наименьшее значение функции на отрезке:
2. Исследовать функцию и построить ее график:
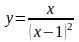
Вариант 2
1.
Найти наибольшее и наименьшее значение
функции на отрезке:
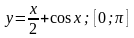
2. Исследовать функцию и построить ее график:
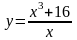
Вариант 3
1.
Найти наибольшее и наименьшее значение
функции на отрезке:
2. Исследовать функцию и построить ее график:
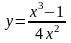
Вариант 4
1.
Найти наибольшее и наименьшее значение
функции на отрезке:
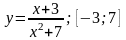
2. Исследовать функцию и построить ее график:
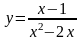
Вариант 5
1.
Найти наибольшее и наименьшее значение
функции на отрезке:
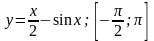
2. Исследовать функцию и построить ее график:
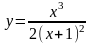
Вариант 6
Найти наибольшее и наименьшее значение функции на отрезке:
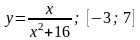
Исследовать функцию и построить ее график:
Вариант 7
Найти наибольшее и наименьшее значение функции на отрезке:
Исследовать функцию и построить ее график:
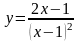
Вариант 8
Найти наибольшее и наименьшее значение функции на отрезке:
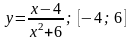
Исследовать функцию и построить ее график:
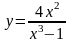
Вариант 9
Найти наибольшее и наименьшее значение функции на отрезке:
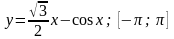
Исследовать функцию и построить ее график:
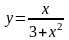
Вариант 10
Найти наибольшее и наименьшее значение функции на отрезке:
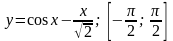
Исследовать функцию и построить ее график:
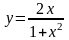
Вариант 11
1. Найти наибольшее и наименьшее значение функции на отрезке:
;
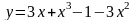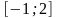
2. Исследовать функцию и построить ее график:
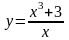
Вариант 12
1. Найти наибольшее и наименьшее значение функции на отрезке:
;
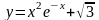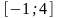
2. Исследовать функцию и построить ее график:
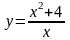
Вариант 13
1. Найти наибольшее и наименьшее значение функции на отрезке:
;
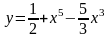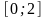
2. Исследовать функцию и построить ее график:
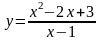
Вариант 14
1. Найти наибольшее и наименьшее значение функции на отрезке:
;
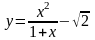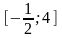
2. Исследовать функцию и построить ее график:
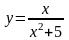
Вариант 15
1. Найти наибольшее и наименьшее значение функции на отрезке:
;
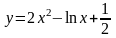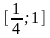
2. Исследовать функцию и построить ее график:
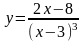
Вариант 16
1. Найти наибольшее и наименьшее значение функции на отрезке:
;
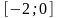
2. Исследовать функцию и построить ее график:
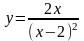
Вариант 17
1. Найти наибольшее и наименьшее значение функции на отрезке:
;
2. Исследовать функцию и построить ее график:
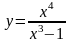
Вариант 18
1. Найти наибольшее и наименьшее значение функции на отрезке:
;
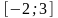
2. Исследовать функцию и построить ее график:
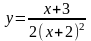
Тема 7. Интегральное исчисление функции одной переменной.
Вариант 1.
Задание 1: Вычислить интегралы:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
з)
|
и)
|
Задание 2:
Вычислить
площадь фигуры, ограниченной параболами:
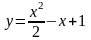и
.
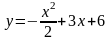Вариант 2.
Задание 1: Вычислить интегралы:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
з)
|
и)
|
Задание
2:
Вычислить площадь фигуры, заключенной
между кривой
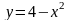и осью.
Вариант 3.
Задание 1: Вычислить интегралы:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
з)
|
и)
|
Задание
2:
Вычислить объем тела, полученного
вращением вокруг оси
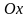фигуры, ограниченной параболой
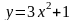и прямой
.
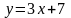Вариант 4.
Задание 1: Вычислить интегралы:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
з) |
и)
|
Задание
2:
Вычислить объем тела, образованного
вращением вокруг оси
фигуры, ограниченной параболой
,
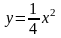прямой
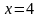и осью
.
Вариант 5.
Задание 1: Вычислить интегралы:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
з)
|
и)
|
Задание
2:
Вычислить площадь фигуры, ограниченной
гиперболой
,
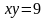осью ОХ
и прямыми
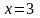и
.
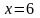Вариант 6.
Задание 1: Вычислить интегралы:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж) |
з)
|
и)
|
Задание
2:
Вычислить площадь фигуры, ограниченной
линиями
,
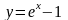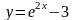и осью
.
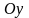Вариант 7.
Задание 1: Вычислить интегралы:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
з)
|
и) |
Задание
2:
Вычислить площадь фигуры, ограниченной
параболой
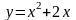и прямой
.
Вариант 8.
Задание 1: Вычислить интегралы:
а)
|
б)
|
в)
|
г)
|
д)
|
е)
|
ж)
|
з)
|
и)
|
Задание
2:
Вычислить объём тела, образованного
вращением фигуры, ограниченной линиями
,
,
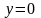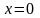вокруг оси
.
Вариант 9.
Задание 1: Вычислить интегралы:
а)
|
б)
|
в)
|
г)
|
д)
|
е) |
ж)
|
з)
|
и)
|
Задание
2:
Вычислить объём тела, образованного
вращением фигуры, ограниченной параболой
,
прямой
,
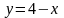вокруг оси
.
Питання до іспиту
Рівняння прямої лінії на площині.
Коло, його рівняння і властивості.
Еліпс, його рівняння і властивості.
Гіпербола, її рівняння і властивості.
Парабола, її рівняння і властивості.
Визначення матриці. Дії над матрицями.
Визначники 2-го і 3-го порядки. Властивості визначників.
Мінор, алгебраїчне доповнення.
Обернена матриця і її знаходження.
Системи лінійних рівнянь. Формули Крамера.
Рішення систем рівнянь методом Гауса і матричним методом.
Функціональна залежність. Способи завдання функції. Основні властивості функцій.
Похідна, її фізичне, геометричне і економічне значення.
Формули диференціювання.
Складна функція. Знаходження похідних складних функцій.
Зростання і убування функції. Ознаки зростання і убування функції.
Екстремуми функції. Теорема Ферма (необхідна ознака екстремуму).
Достатня ознака існування екстремуму.
Опуклість і угнутість кривої. Точка перегину. Необхідні і достатні умови існування точки перегину.
Побудова графіків і функцій по характерних точках.
Задачі на максимум і мінімум.
Функції багатьох змінних. Частинні похідні функцій.
Первісна функція і невизначений інтеграл.
Властивості невизначеного інтеграла.
Таблиця найпростіших інтегралів.
Основні методи інтегрування.
Визначений інтеграл. Формула Ньютона-Лейбніца. Основні властивості визначеного інтеграла.
Методи обчислення визначеного інтеграла.
Геометричне і економічне значення визначеного інтеграла.
Обчислення площ плоских фігур і об’ємів тіл обертання за допомогою визначеного інтеграла.