Билет № 37. Понятие функции нескольких переменных. Область определения. Частные производные первого порядка и их геометрический смысл.

Функции нескольких переменных.

Определение. Если каждой паре (x,y) значений двух независимых друг от друга, переменных величин x и y, из некоторой области их изменения D, соответствует определенное значение величины z, то говорят, что z функция двух независимых переменных x и y, определенная в области D.

Обычно функция нескольких переменных задается явным аналитическим способом. Например: z=3x+5y²,u=xy+z² и т.д.

Встречается также и неявное задание таких функций, например: z-2x-sinxy=0.

 Упорядоченная пара чисел (x,y) может рассматриваться как точка на плоскости, т.е. Z есть функция точки (x,y).

Чтобы задать функцию z=f(x,y), надо не только указать правило нахождения z по заданным x и y, но и то множество (называемое областью задания функции) пар значений, которые могут принимать аргументы x и y.

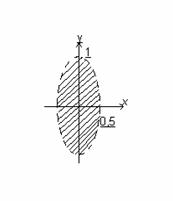
Например, функция z= задана только при 1-y >0, т.е. внутри эллипса y²+4x²<1 с полуосями, а=0,5 и в=1 не включая точки, лежащие на эллипсе.

 

Определение. Если каждой совокупности значений переменных x,y,z…t соответствует определенное значение переменной w, то w называется функцией независимых переменных x,y,z…t и записываетсяw=f(x,y,z…t).

Для функции трех переменных областью определения является упорядоченная тройка чисел (x,y,z), т.е. некоторая совокупность точек пространства. Область определения функции четырех и большего числа переменных не допускает простого геометрического истолкования.

Функции двух переменных допускают графическую иллюстрацию. Графиком функции z=f(x,y), заданной на некотором множестве D точек плоскости ХОУ, называется множество точек (x,y,z) пространства, у которых (x,y) принадлежит D, аz=f(x,y). В наиболее простых случаях такой график представляет собой некоторую поверхность.

Например, графиком функции z=4-x²-y² является параболоид.

 

Функции трех и большего числа переменных не имеют геометрического представления.

Область определения.

Областью определения функции   (выражения f(x) ) называют множество всех значений x , для которых функция (выражение) имеет смысл. Область определения функции   обозначается как   или  .  При нахождении области определения функции приходится решать различные неравенства (иррациональные, логарифмические, тригонометрические и т.п.) и системы неравенств.

Частные производные первого порядка и их геометрический смысл.

Пусть задана функция z = ƒ (х; у). Так как х и у — независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение Δх, сохраняя значение у неизменным. Тогда z получит приращение, которое называется частным приращением z по х и обозначается ∆_хz. Итак,

Δ_хz=ƒ(х+Δх;у)-ƒ(х;у).

Аналогично получаем частное приращение z по у:

Δ_уz=ƒ(x;у+Δу)-ƒ(х;у).

Полное приращение Δz функции z определяется равенством

Δz = ƒ(х + Δх;у + Δу)- ƒ(х; у).

 Если существует предел

то он называется частной производной функции z = ƒ (х; у) в точке М(х;у) по переменной х и обозначается одним из символов:

Частные производные по х в точке М₀(х₀;у₀) обычно обозначают символами

Аналогично определяется и обозначается частная производная от z=ƒ(х;у) по переменной у:

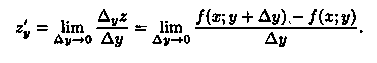
Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции ƒ(х;у) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной величиной).

 

и частные производные функции z = 2у + е^{х2-у +1}. Решение:

 

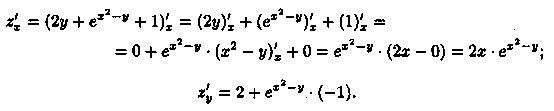
Г еометрический смысл частных производных функции двух переменных

Графиком функции z= ƒ (х; у) является некоторая поверхность (см. п. 12.1). График функции z = ƒ (х; у₀) есть линия пересечения этой поверхности с плоскостью у = у_о. Исходя из геометрического смысла производной для функции одной переменной (см. п. 20.2), заключаем, что ƒ'x(х_о;у_о) = tg а, где а — угол между осью Ох и касательной, проведенной к кривой z = ƒ (х; у₀) в точке Мо(хо;уо; ƒ(хо;уо)) (см. рис. 208).

Аналогично, f'y (х₀;у₀)=tgβ.