Ответы на билеты по математическому анализу Билет №1. Множества и операции над ними

Понятие множества является фундаментальным неопределимым понятием.

Интуитивно под множеством будем понимать собрание определенных вполне различимых объектов, рассматриваемых как единое целое. Отдельные объекты, из

которых состоит множество, называются элементами его. Для обозначения конкретных множеств используются прописные (возможно с индексами) буквы

A, X , A1, X1, для обозначения элементов множества используются строчные (возможно с индексами) буквы x, a, x1,a1. Если x − элемент множества X , то пишут x∈ X (∈− символ принадлежности). Множество, не имеющее ни одного элемента, называют пустым множеством (обозначается Ø). Множество может быть задано перечислением или описанием. Задание множества перечислением заключается в составлении полного списка всех входящих в это множество элементов, заключенных

в фигурные скобки. Например, множества N ={1;2;3;...}, Z ={0;±1;±2;...} − это заданные перечислением множества натуральных и целых чисел соответственно. Задание множества описанием состоит в записи всех свойств его элементов, заключенных в фигурные скобки. Например, множества Q = {х = p/q; p ∈Z; q ∈ N}, I ={x∈ R; x − числа с бесконечной непериодической дробной частью}} –это множества рациональных и иррациональных чисел соответственно, заданные описательно. Множество B называют подмножеством множества A (обозначается B ⊆ A), если любой элемент множества B (∀b :b∈B) является элементом множества A. Если хотят подчеркнуть, что множество A содержит элементы, не принадлежащие B (a∈ A, a∉B), то пишут B ⊂ A (⊂ − символ строгого включения ) .

Например, N ⊂ Z ⊂ Q ⊂ I ⊂ R. Два множества A и B называются равными (обо-

значается A = B ), если одновременно A⊆ B и B ⊆ A. Пересечением или произ-

ведением двух множеств A и B называется множество C (обозначается

C = A I B ), состоящее из всех тех и только тех элементов, которые принадлежат

как множеству A, так и множеству B . Множества A и B называются непересекаю-

щимися, если A I B =Ø. Объединением или суммой двух множеств A и B называ-

ется множество D (обозначается D = A U B ), состоящее из всех тех и только тех

элементов, которые принадлежат или A, или B . Например,

Q U I = R = (−∞;∞) −множество всех действительных чисел. Разностью множеств

A и B называется множество E (обозначается E = A \ B), состоящее из всех эле-

ментов множества A, которые не принадлежат множеству B . Приведем некоторые

свойства операций объединения и пересечения множеств и два полезных обозна-

чения:

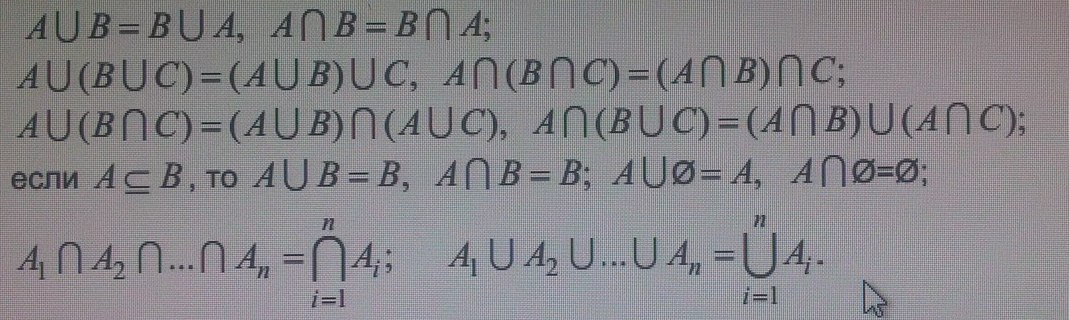
Множество называется конечным, если число его элементов конечно, Множество

называется счетным, если число его элементов бесконечно, но между ними и эле-

ментами множества N можно установить взаимнооднозначное соответствие. В про-

тивном случае бесконечное множество называется несчетным. Счетными множест-

вами являются, например, числовые множества Z и Q , а несчетными – любой ин-

тервал или объединение интервалов и множество R .

Билет №2. Числовая последовательность и её предел.

Числовая последовательность — это последовательность элементов числового пространства.

Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.

Определение. Пусть каждому натуральному числу n поставлено в соответствие некоторое единственное действительное число  (при этом разным натуральным числам n могут соответствовать и одинаковые действительные числа). В этом случае на множестве натуральных чисел определена функция:  , которая называется числовой последовательностью или просто последовательностью.

Последовательность обозначается:  , n=1, 2,… или  .

Числа  ,  ,… называются членами последовательности или ее элементами,  – общим членом последовательности, n – номером члена  .

По определению любая последовательность содержит бесконечное множество элементов.

Часто последовательность задается при помощи формулы:  ,  . В этом случае эта формула называется формулой общего члена последовательности { }. Например,  = , ;

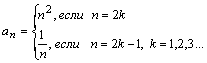
Последовательность может быть задана и другими способами. Например, если   – число всех различных делителей числа n, то  ,  - последовательность, для которой  =1,  =2,  =2,  =3,  =2,  =4,  =2,…

Для задания последовательностей используют также рекуррентные соотношения. При таком способе задания последовательности указывают один или несколько первых ее членов и формулу, которая позволяет найти ее n-й член через предшествующие члены. Например,

a =1, a =  +1 при n=1, 2,…;

b =1, b =2, b =2b +b  при n 3.

Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу  a  при увеличении порядкового номера  n. В этом случае говорят, что числовая последовательность имеет предел. Это понятие имеет более строгое определение.

Это определение означает, что  a  есть предел числовой последовательности, если её общий член неограниченно приближается к  a  при возрастании  n. Геометрически это значит, что для любого   > 0  можно найти такое число N,  что начиная с  n > N  все члены последовательности расположены внутри интервала ( a  a   ). Последовательность, имеющая предел, называется сходящейся; в противном случае – расходящейся.

Последовательность называется ограниченной, если существует такое число M, что | u_n  |  Mдля всех  n . Возрастающая или убывающая последовательность называется монотонной.

Теорема Вейерштрасса. Всякая монотонная и ограниченная последовательность имеет предел (эта теорема даётся в средней школе без доказательства). 

Основные свойства пределов.  Нижеприведенные свойства пределов справедливы не только для числовых последовательностей, но и для функций.

Если { u_n } и { v_n }   две сходящиеся последовательности, то:

Если члены последовательностей { u_n }, { v_n }, { w_n } удовлетворяют неравенствам