10. Потеря устойчивости в большом и малом

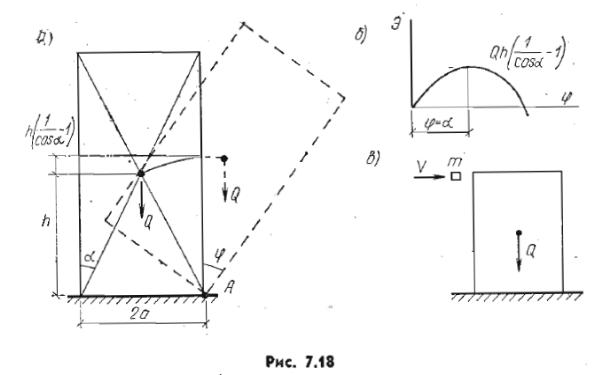
Если стержень или стержневая констр., выведенная из равновесия, вновь возвращ. В свое первонач. Положение, то такое состояние считается устойчивым. При определенном значении силы (Ркр) выведенный из состояния равновесия стержень, уже не возвращается в исходное положение. Такое состояние системы будет неустойчивым. (на всякий случай  : при Р=Ркр происходит разветвление форм равновесия – бифуркация. Это означает, что одной и той же нагрузке может соответствовать две формы равновесия, или деф. Состояния.)

Для нелинейных систем введены понятия устойчивости "в малом", "в большом", "в целом". Система устойчива "в малом", если она устойчива при малых (бесконечно малых) начальных отклонениях (т.е. если она возвращается в состояние равновесия после любого малого возмущения, а в переходном состоянии величины координат системы получают малые отклонения от первоначально заданных.). Система устойчива "в большом", если она устойчива при больших (конечных по величине) начальных отклонениях(если она возвращается в состояние равновесия после любых отклонений от исходного номинального режима). Система устойчива "в целом", если она устойчива при любых больших (неограниченных по величине) начальных отклонениях. На рис.7.3 приведены фазовые траектории систем: устойчивой "в целом" (а) и системы устойчивой "в большом" и неустойчивой "в малом" (б);

11. Случайные функции. Основные характеристики случайной функции

В отличие от числовых характеристик случайных величин, предоставляющих собой определенные числа, характеристики случайных функций представляют собой в общем случае не числа, а функции

12. Применение метода перемещений для расчета на устойчивость рам

При рассмотрении вопросов устойчивости рам так же, как и других систем, необходимо различать два типа задач:

потеря устойчивости 1-го рода (потери устойчивости в Эйлеровском смысле) и

потеря устойчивости 2-го рода (потеря несущей способности сжато-изогнутой рамы).

Постановка задачи и схема решения при расчете на устойчивость l-го рода

Для исследования устойчивости рамы принимаются следующие допущения:

1. Рассматривается только узловая нагрузка, не вызывающая поперечного изгиба стерж­ней рамы.

2. Стержни считаются нерастяжимыми и несжимае­мыми.

3. Изменением расстояния между концами стержня, которое получается благодаря его изгибу, пренебре­гаем.

4. При работе учитываются нормальные силы, возни­кающие до потери устойчивости. Влияние приращений нормальных сил ΔN, возникающих в момент потери ус­тойчивости, не учитывается.

5. При определении поперечных сил в изогнутых стержнях не учитывается изменение угла наклона сечения за счет изгиба стержня.

В расчетах на устойчивость для большинства типов рам метод перемещений требует более простых и менее трудоемких вычислений, чем метод сил.

Как показано, расчет рам на устойчивость l-го рода методом перемещений сводится к составлению си­стемы однородных канонических уравнений этого метода и приравниванию нулю определителя, составленного из коэффициентов при неизвестных. Для облегчения опре­деления коэфицентов типа r_ik и R_ip (последние будут нужны при деформационном расчете) при наличии продольной силы в стержне однопролетные балки различных типов рассчитаны заранее при помощи формул на различные виды воздействий.

Таким образом получена таблица реакций сжатоизо­гнутых стержней от единичных перемещений и нагрузок которой и надлежит пользоваться при практи­ческих расчетах.

ПРИМЕР 11: 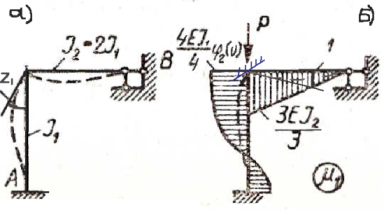Требуется найти Ркр для рамы, показанной на рисунке 31а. Основная система метода перемещений и эпюра изгибающих моментов от единичного поворота узла 1, показаны на рисунке 31б.

При построении эпюры продольная сила в ригеле (в соответсвии с принятым выше допущением) считалось равным нулю, продольная сила в стойке равна Р. Каноническое уравнение метода перемещений имеет вид: r₁₁z₁=0. Так как мы ищем олько нагрузку, соттветсвующую изогнутому равновесному состоянию рамы, то z₁ ≠0. Следовательно

Откуда EI₁(φ₂(𝑣)+2)=0 и φ₂(𝑣)=-2.

По таблице значений φ₂(𝑣)=-2 находим по интерполяции 𝑣=5,66. Критическая нагрузка . Коэфицент свободной длины стойки может быть найден при приравнивании полученного значения критической силы критической силе по формуле Эйлера:

откуда В нашем случае , т.е. стойка работает в условиях, близких к полному защемлению верхнего конца (как и следовало ожидать, ввиду большой жесткости ригеля).

Расчетная длина стойки l₀=𝛍l=0.555·4=2.22м является исходной величиной для нахождения коэфицента продольного изгиба φ в зависимости от расчетной гибкости и материала стержня по таблицам из соответствующих СНиП.