Вопрос 65-66: Общее равновесие и эффективность в производстве. Эффективность структуры выпуска.
Рассмотрим эффективные по Парето способы осуществления выбора между технологически допустимыми потребительскими наборами.
Обозначим совокупные потребительские наборы через (X1, X2284). Это означает, что в наличии для потребления имеются X1285 единиц товара 1 и X2286 единиц товара 2. В экономике Зная общее количество каждого товара, можно нарисовать ящик Эджуорта, как на рис.29.9.
При заданном (X1, X2287) множество потребительских наборов, эффективных по Парето, будет множеством такого же рода, как и множества, рассмотренные в предыдущей главе: как показано на рис.29.9, объемы потребления, эффективные по Парето, будут лежать на множестве Парето — линии взаимных касаний кривых безразличия. Это такие распределения, при которых предельная норма замещения каждого потребителя — пропорция, согласно которой он как раз готов совершить обмен — равна предельной норме замещения другого потребителя.
Указанные распределения являются эффективными по Парето в том, что касается решений о потреблении. Если люди могут просто обменять один товар на другой, то множество Парето описывает множество наборов, исчерпывающее выгоды от обмена. Однако в экономике, где имеет место не только обмен, но и потребление, существует другой способ обменять один товар на другой, а именно: произвести меньше одного товара и больше другого.
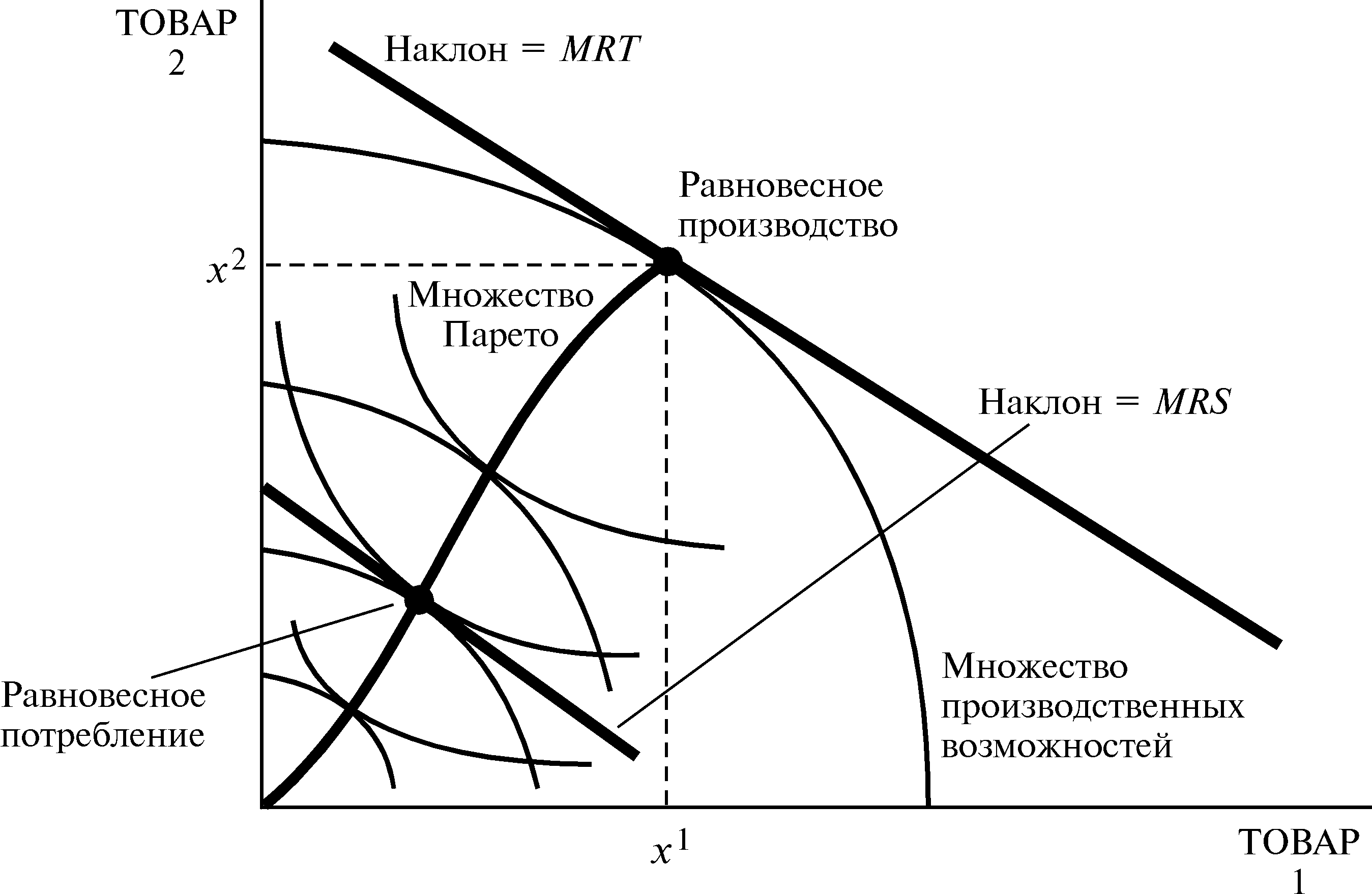
Рисунок 29.9 Производство и ящик Эджуорта.
Множество Парето описывает множество наборов, эффективных по Парето, при заданных наличных количествах товаров 1 и 2, однако, в экономике, где имеется производство, сами эти количества могут быть выбраны из множества производственных возможностей. Какие варианты выбора из множества производственных возможностей будут эффективными по Парето?
Представим себе логику, лежащую в основе условия, связанного с предельной нормой замещения. Как нами утверждалось, в точке распределения, эффективного по Парето, MRS потребителя A должна равняться MRS потребителя B: пропорция, в которой потребитель A как раз хотел бы обменять один товар на другой, должна быть равна пропорции, в которой потребитель B как раз готов обменять один товар на другой. Если бы это было не так, то существовала бы какая-то обменная сделка, в результате которой повысилось бы благосостояние обоих потребителей.
Вспомним, что предельная норма трансформации (MRT) измеряет пропорцию, в которой можно "превратить" один товар в другой. Конечно, в действительности не происходит буквального превращения одного товара в другой. Происходит, скорее, перемещение факторов производства с тем, чтобы производить меньше одного товара и больше другого.
Предположим, что экономика функционирует в точке, где предельная норма замещения у одного из потребителей не равна предельной норме трансформации одного товара в другой. В таком случае указанная точка не может быть эффективной по Парето. Почему? Потому что в этой точке пропорция, в которой потребитель готов обменять товар 1 на товар 2, отличается от пропорции, в которой товар 1 может быть превращен в товар 2 — существует способ повысить благосостояние данного потребителя, изменив структуру производства.
Допустим, например, что MRS данного потребителя равна 1; потребитель готов заменить товар 2 товаром 1 в пропорции один к одному. Допустим, что MRT равна 2; это означает, что отказ от одной единицы товара 1 позволит обществу произвести две единицы товара 2. Поскольку потребителю безразлично, отказаться от одной единицы товара 1, получив взамен одну единицу другого товара, или нет, его благосостояние, конечно, повысится, если он получит две добавочные единицы товара 2.
Этот же довод можно привести всегда, когда у одного из потребителей MRS отлична от MRT — в этом случае всегда можно произвести перестройку потребления и производства, в результате которой благосостояние данного потребителя повысится. Как мы уже видели, в ситуации, эффективной по Парето, MRS каждого потребителя должна быть одной и той же, а из приведенных выше рассуждений следует, что MRS каждого потребителя должна, фактически, равняться MRT.
Рис.29.9 иллюстрирует распределение, эффективное по Парето. MRS у всех потребителей одинаковы, так как их кривые безразличия в ящике Эджуорта касаются друг друга. И MRS каждого потребителя равна MRT — наклону границы множества производственных возможностей.
Алгебраическая формализация модели
Выведем условия эффективности по Парето в экономике, где имеется не только обмен, но и производство, воспользовавшись дифференциальным исчислением. Пусть X1288 и X2289 представляют, как в основной части главы, общее произведенное и потребленное количество товаров 1 и 2:
X1
=
X2
=
.
Первое, что нам требуется, — это найти удобный способ описания границы производственных возможностей, т.е. всех технологически допустимых комбинаций X1290 и X2291. Для наших целей удобнее всего сделать это, воспользовавшись функцией трансформации. Это функция совокупных количеств двух товаров T(X1, X2)292, таких, что комбинация 293(X1, X2) находится на границе производственных возможностей (границе множества производственных возможностей), если и только если
T(X1, X2) = 0.
Описав технологию, можно вычислить предельную норму трансформации — пропорцию, в которой мы должны пожертвовать товаром 2, чтобы произвести больше товара 1. Хотя данное название и вызывает в представлении картину "превращения" одного товара в другой, эта картина несколько обманчива. На самом деле происходит перемещение ресурсов из производства товара 2 в производство товара 1. Таким образом, уделяя меньше ресурсов производству товара 2 и больше — производству товара 1, мы перемещаемся из одной точки на границе производственных возможностей в другую. Предельная норма трансформации есть не что иное, как наклон границы множества производственных возможностей, обозначаемый нами как dX2/dX1.
Рассмотрим малое изменение производства (dX1, dX2294), остающееся практически осуществимым. Мы получаем поэтому следующее уравнение:
dX1
+
dX2
= 0.
Найдя из него предельную норму трансформации, получаем
=
—
.
В случае для двух индивидов можно записать указанную задачу максимизации как
max
uA(
,
)295
при
uB
(
,
)
=
296
T(X1, X2) = 0.
Функция Лагранжа для данной задачи имеет вид
L = uA ( , ) — (uB ( , ) — ) —
— (T(X1, X2) — 0),
а условия первого порядка — вид
—
=
0,
—
=
0
=
—
—
=
0
=
—
—
=
0.
Выполнение преобразований и деление первого уравнения на второе дает нам
.
Выполнение той же самой операции над третьим и четвертым уравнениями дает
.
Левые части этих уравнений — предельные нормы замещения. Правая часть этих уравнений — предельная норма трансформации. Таким образом, указанные уравнения требуют, чтобы у каждого индивида предельная норма замещения для двух товаров равнялась предельной норме трансформации: пропорция, в которой каждый индивид готов заместить один товар другим, должна быть той же, что и пропорция, в которой превращение одного товара в другой является технологически допустимым. Предположим, что MRS для какого-то индивида не равна MRT. Тогда пропорция, в которой данный индивид был бы готов пожертвовать одним товаром ради получения большего количества другого, отличалась бы от пропорции, в которой превращение одного товара в другой является технологически допустимым — но это означает, что существовал бы какой-то способ увеличения полезности для данного индивида, не затрагивающий чьего-либо еще потребления.