Вопрос 52: Ценообразование по схеме двойного тарифа.
Суть данной схемы ценообразования состоит в следующем: с потребителей взимается, во-первых, фиксированная ''входная'' плата за доступ к потреблению данного товара, а во-вторых, плата (одинаковая) за каждую потребленную единицу товара.
Имеется множество других применений двойных тарифов: Polaroid продает фотоаппарат по одной цене, а пленку — по другой. Принимая решение о том, покупать фотоаппарат или нет, люди, предположительно, учитывают и стоимость пленки. Компания, производящая лезвия для бритья, продает бритву по одной цене, лезвия — по другой — и снова цена, устанавливаемая ею на лезвия, влияет на спрос на бритвы, и наоборот.
Рассмотрим решение этой задачи ценообразования в контексте исходного примера задачи, называемой дилеммой Диснейленда. Как обычно, примем ряд упрощающих предпосылок. Во-первых, полагаем, что в Диснейленде имеется только один вид аттракционов; во-вторых, что вкусы всех посетителей в отношении аттракционов одинаковы.
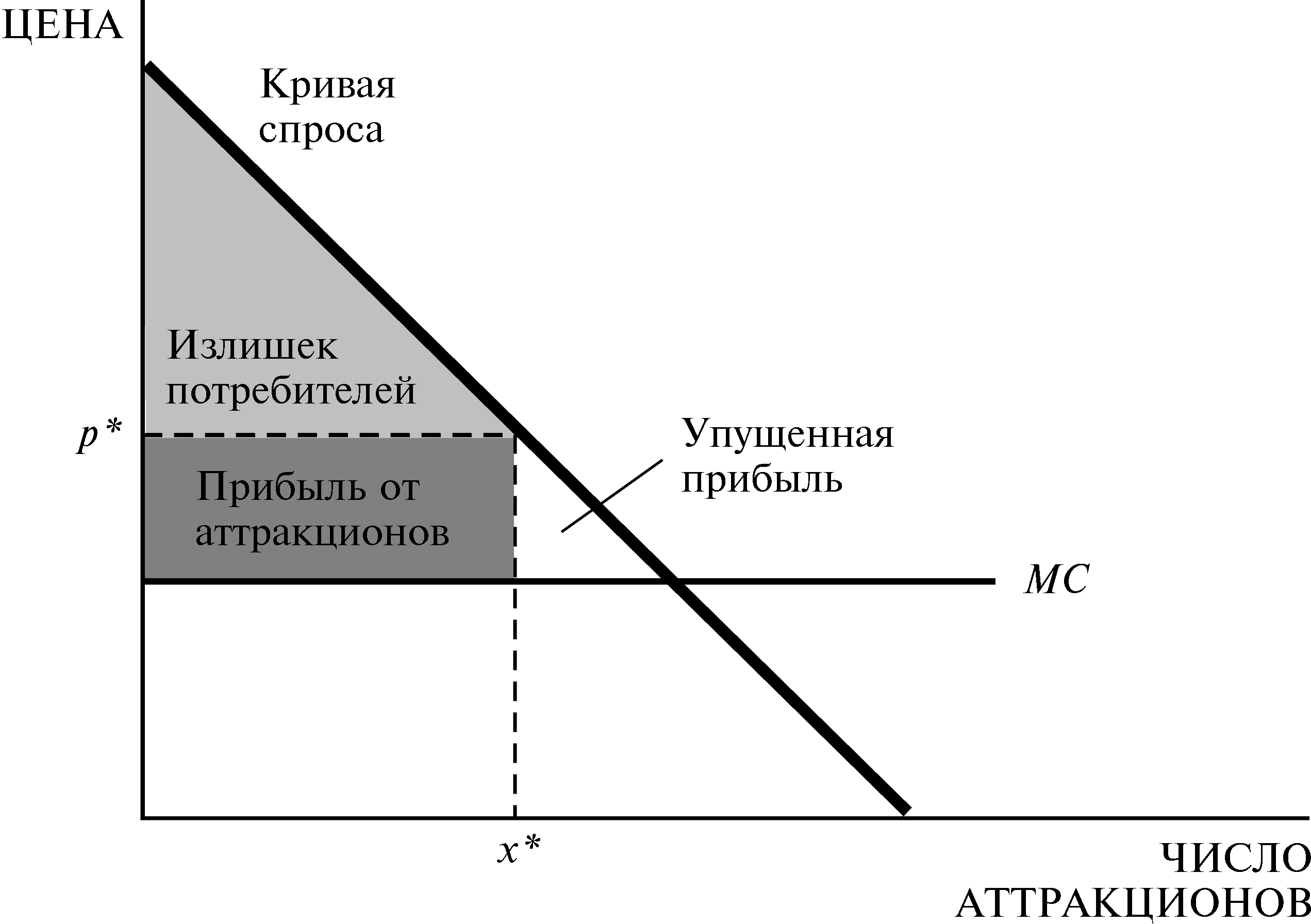
На рис.24.5 изображены кривая спроса и кривая предельных издержек (постоянных) на аттракционы. Как обычно, кривая спроса нисходящая: если Диснейленд установит на каждый аттракцион высокую цену, будет куплено меньше аттракционов. Предположим, что владельцы парка устанавливают на аттракцион цену p*125, как на рис.24.5; результатом этого является спрос на x*126 аттракционов. Какую цену за вход в парк смогут установить его владельцы, если цена аттракционов составляет p*127?
Общая готовность платить за x*128129 аттракционов измеряется излишком потребителей. Следовательно, самое большее, что могут запросить за вход владельцы парка, это — площадь, обозначенная "излишек потребителей" на рис.24.5. Общую прибыль монополиста составит эта площадь плюс прибыль от аттракционов (p* — AC)x*130131, но так как в данной модели издержки постоянны, то MC = AC, и выражение (p* — AC)x* можно переписать в виде (p* — MC)x*
|
Дилемма Диснейленда. Если владельцы парка установят цену p*132133, то спрос на аттракционы составит x*134135. Излишек потребителей измеряет цену, которую владельцы могут установить за вход в парк. Общая прибыль фирмы максимизируется, когда владельцы устанавливают цену, равную предельным издержкам. |
Рис. 24.5 |
Нетрудно увидеть, что общая прибыль максимизируется при цене, равной предельным издержкам: как мы видели ранее, эта цена дает максимально возможный излишек потребителя плюс излишек производителя. Поскольку монополист получает возможность затребовать у людей их излишек потребителей, установление цены, равной предельным издержкам, и платы за вход, приводящей к извлечению излишка потребителей, есть политика максимизации прибыли.
И действительно, именно этой политики придерживаются Диснейленд и большинство других парков аттракционов. Существует единая плата за вход, но зато аттракционы внутри парка бесплатные. Похоже, что предельные издержки на аттракционы меньше, чем транзакционные издержки сбора отдельной платы за них.
Алгебраически данную модель можно формализовать следующим образом:
Прибыль (П) при данной схеме ценообразования есть сумма прибыли от входной платы Пе и прибыли от продаж Пs.
Запишем условие максимизации прибыли:
Max П = Пе+(p — AC)(x1+x2)
То есть если на рынке действует две группы покупателей с линейными кривыми спроса вида x1 = a — bp1136 и x2 = c — dp2137138, то выражение примет следующий вид:
Max П = CS1(p)+CS2(p)+(p — AC)(x1+x2),
Где CS1(p1) и CS2(p2) – потребительские излишки соответственно первой и второй групп покупателей, выраженные как функция от цены, а x1+x2 – функция совокупного спроса.
Решив уравнение максимизации (частная производная прибыли по цене), мы найдем цену и размер потребительских излишков, больший из которых и будет равен Пе.